Invoking the sequence analysis lemma (A) on

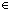
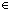
n  , p, q  Peg, a  , z  {a...}, s  {a...z}{1...n}Peg

gives us x  {a...z-1}, y  {x+1...z}, p', q'  Peg such that

(F) u:{a...x}. s(u,n) = p

(G) u:{y...z}. s(u,n) = q

(H) s(x) = (i.p')  {1...n-1}Peg

(I) s(y) = (i.q')  {1...n-1}Peg

(J) p  p'

(K) q  q'

In anticipation of applying the inductive hypothesis note two lemmas about slicing a Hanoi sequnce vertically or horizontally.

Thm*  n':, n:{n'...}, a:, z:{a...}, s:({a...z}{1...n}Peg).
Thm*  s is a Hanoi(n disk) seq on a..z
Thm*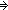  
Thm*  (x:{a...z}, i:{n'+1...n}. s(a,i) = s(x,i))
Thm*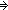  
Thm*  s is a Hanoi(n' disk) seq on a..z

Thm*  n:, a,z:, s:({a...z}{1...n}Peg).
Thm*  s is a Hanoi(n disk) seq on a..z
Thm*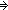  
Thm*  (a',z':{a...z}. s is a Hanoi(n disk) seq on a'..z')

The first of these says that a Hanoi sequence for one set of disks is also a Hanoi sequence for smaller disks so long as the larger disks are left untouched. The second one says that chopping states off the front and back leaves you with a Hanoi sequence. Applying these lemmas to (C) s is a Hanoi(n disk) seq on a..z allows to infer both

s is a Hanoi(n-1 disk) seq on a..x

s is a Hanoi(n-1 disk) seq on y..z

Then applying the inductive hypothesis (B) to

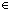
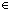
n-1  , p, p'  Peg, a  , x  {a...}, s  {a...z}{1...n}Peg

and then to

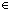
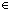
n-1  , q', q  Peg, y  , z  {a...}, s  {a...z}{1...n}Peg

gives us

(2^(n-1))x-a+1 and (2^(n-1))z-y+1

which suffice by arithmetic to entail our goal (*) 2(2^(n-1))z-a+1.

(Hint - compare the right hand sides: (x-a+1)+(z-y+1)z-a+1 since x+1-y0.)

QED

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html