| | Some definitions of interest. |
|
| assert | Def 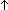 b == if b b == if b True else False fi True else False fi |
| | | Thm*  b: b: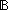 . b . b  Prop Prop |
|
| band | Def p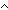 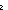 q == if p q == if p q else false q else false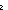 fi fi |
| | | Thm*  p,q: p,q: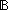 . (p . (p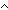 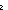 q) q)  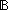 |
|
| decidable | Def Dec(P) == P 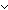 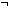 P P |
| | | Thm*  A:Prop. Dec(A) A:Prop. Dec(A)  Prop Prop |
|
| iff | Def P 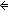  Q == (P Q == (P   Q) & (P Q) & (P 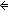  Q) Q) |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A 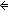  B) B)  Prop Prop |
|
| nat | Def  == {i: == {i: | 0 | 0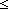 i } i } |
| | | Thm*   Type Type |
|
| nat_plus | Def  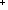 == {i: == {i: | 0<i } | 0<i } |
| | | Thm*  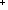  Type Type |
|
| sfa_doc_exteq | Def A =ext B == ( X:A. X X:A. X  B) & ( B) & ( X:B. X X:B. X  A) A) |
|
| sfa_doc_sexpr | Def Sexpr(A) == rec(T.(T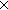 T)+A) T)+A) |
| | | Thm*  A:Type. Sexpr(A) A:Type. Sexpr(A)  Type Type |
|
| top | Def Top == Void(given Void) |
| | | Thm* Top  Type Type |