Selected Objects
| def | action_set | ActionSet(T) == car:Type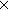 T T 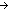 car car  car car |
| def | aset_car | a.car == 1of(a) |
| def | aset_act | a.act == 2of(a) |
| def | factorial | (rec) (n)! == if n= 0 0 1 else n 1 else n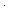 (n-1)! fi (n-1)! fi |
| THM | ex1_of_factorial | (0)! = 1 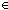 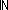 |
| def | multi_action | (rec) multi_action(l; s; ASet)
== if null(l) s else ASet.act(hd(rev(l)),multi_action(ASet.act; rev(tl(rev(l))); s)) fi s else ASet.act(hd(rev(l)),multi_action(ASet.act; rev(tl(rev(l))); s)) fi |
| def | maction | (rec) (S:L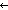 s) == if null(L) s) == if null(L) s else S.act(hd(L),(S:tl(L) s else S.act(hd(L),(S:tl(L)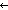 s)) fi s)) fi |
| THM | maction_lemma |  S:ActionSet(Alph), s:S.car, L1,L2,L:Alph*. (S:L1 S:ActionSet(Alph), s:S.car, L1,L2,L:Alph*. (S:L1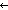 s) = (S:L2 s) = (S:L2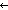 s) s)  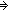 (S:L @ L1 (S:L @ L1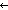 s) = (S:L @ L2 s) = (S:L @ L2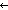 s) s) |
| def | lpower | (rec) (L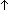 n) == if n= n) == if n= 0 0 nil else (L nil else (L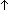 n-1) @ L fi n-1) @ L fi |
| THM | lpower_alt |  L:Alph*, n: L:Alph*, n: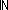 . (L . (L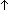 n) = if n= n) = if n= 0 0 nil else L @ (L nil else L @ (L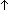 n-1) fi n-1) fi |
| THM | pump_theorem |  S:ActionSet(Alph), N: S:ActionSet(Alph), N: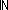  , s:S.car.
#(S.car)=N , s:S.car.
#(S.car)=N  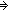 (
( A:Alph*.
N < ||A|| A:Alph*.
N < ||A||  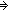 ( (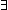 a,b,c:Alph*. 0 < ||b|| & A = ((a @ b) @ c) & ( a,b,c:Alph*. 0 < ||b|| & A = ((a @ b) @ c) & ( k: k: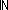 . (S:(a @ (b . (S:(a @ (b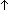 k)) @ c k)) @ c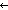 s) = (S:A s) = (S:A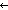 s)))) s)))) |
| THM | pump_thm_cor |  n: n: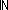 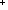 , Alph:Type, S:ActionSet(Alph), s,f:S.car.
#(S.car)=n , Alph:Type, S:ActionSet(Alph), s,f:S.car.
#(S.car)=n  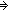 ( (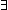 l:Alph*. (S:l l:Alph*. (S:l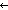 s) = f) s) = f)  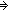 ( (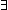 l:Alph*. ||l|| l:Alph*. ||l||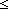 n & (S:l n & (S:l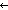 s) = f) s) = f) |
| THM | action_append |  S:ActionSet(T), s:S.car, tl1,tl2:T*. (S:tl1 @ tl2 S:ActionSet(T), s:S.car, tl1,tl2:T*. (S:tl1 @ tl2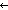 s) = (S:tl1 s) = (S:tl1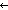 (S:tl2 (S:tl2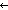 s)) s)) |
| def | n0n1 | n0n1(n) == ([0]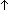 n) @ ([1] n) @ ([1]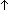 n) n) |
| def | el_counter | (rec) ||e:L|| == if null(L) 0 ;e= 0 ;e= hd(L) hd(L) 1+||e:tl(L)|| else ||e:tl(L)|| fi 1+||e:tl(L)|| else ||e:tl(L)|| fi |
| THM | counter_of_nil |  e: e: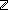 . ||e:nil|| = 0 . ||e:nil|| = 0   |
| THM | counter_append |  e: e: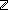 , L,M: , L,M: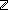 *. ||e:L @ M|| = ||e:L||+||e:M|| *. ||e:L @ M|| = ||e:L||+||e:M|| 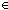 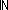 |
| THM | counter_lpower |  e: e: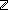 , L: , L: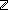 *, n: *, n: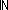 . ||e:(L . ||e:(L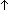 n)|| = n n)|| = n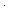 ||e:L|| ||e:L|| 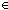 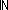 |
| THM | n0n1_irregular |  S:ActionSet( S:ActionSet(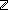 ), s,q:S.car.
( ), s,q:S.car.
(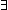 n: n: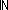  . #(S.car)=n ) & ( . #(S.car)=n ) & ( k: k: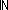 . (S:n0n1(k) . (S:n0n1(k)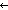 s) = q) s) = q)  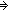 ( (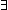 L: L: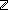 *. (S:L *. (S:L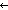 s) = q & ( s) = q & ( k: k: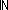 . . 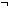 L = n0n1(k))) L = n0n1(k))) |