| multi_action |
Def multi_action(l; s; ASet)
== if null(l) s
else ASet.act(hd(rev(l)),multi_action(ASet.act; rev(tl(rev(l))); s)) fi
(recursive) s
else ASet.act(hd(rev(l)),multi_action(ASet.act; rev(tl(rev(l))); s)) fi
(recursive)
|
| reverse |
Def rev(as) == Case of as; nil  nil ; a.as' nil ; a.as'  rev(as') @ [a] (recursive) rev(as') @ [a] (recursive)
Thm*  T:Type, as:T*. rev(as) T:Type, as:T*. rev(as) 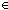 T* T*
|
| tl |
Def tl(l) == Case of l; nil  nil ; h.t nil ; h.t  t t
Thm*  A:Type, l:A*. tl(l) A:Type, l:A*. tl(l) 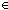 A* A*
|
| aset_act |
Def a.act == 2of(a)
Thm*  T:Type, a:ActionSet(T). a.act T:Type, a:ActionSet(T). a.act 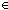 T T  a.car a.car 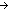 a.car a.car
|
| hd |
Def hd(l) == Case of l; nil  "?" ; h.t "?" ; h.t  h h
Thm*  A:Type, l:A*. ||l|| A:Type, l:A*. ||l||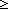 1 1  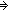 hd(l) hd(l) 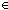 A A
|
| null |
Def null(as) == Case of as; nil  true true ; a.as' ; a.as'  false false
Thm*  T:Type, as:T*. null(as) T:Type, as:T*. null(as) 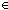 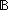
Thm* null(nil) 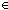 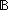
|
| append |
Def as @ bs == Case of as; nil  bs ; a.as' bs ; a.as'  a.(as' @ bs) (recursive) a.(as' @ bs) (recursive)
Thm*  T:Type, as,bs:T*. (as @ bs) T:Type, as,bs:T*. (as @ bs) 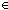 T* T*
|
| pi2 |
Def 2of(t) == t.2
Thm*  A:Type, B:(A A:Type, B:(A 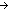 Type), p:a:A Type), p:a:A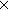 B(a). 2of(p) B(a). 2of(p) 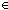 B(1of(p)) B(1of(p))
|
![]() T:Type, as:T*. rev(as)
T:Type, as:T*. rev(as) ![]() T*
T*![]() A:Type, l:A*. tl(l)
A:Type, l:A*. tl(l) ![]() A*
A*![]() T:Type, a:ActionSet(T). a.act
T:Type, a:ActionSet(T). a.act ![]() T
T![]()
![]() a.car
a.car![]()
![]() a.car
a.car![]() A:Type, l:A*. ||l||
A:Type, l:A*. ||l||![]() 1
1 ![]()
![]() hd(l)
hd(l) ![]() A
A![]() T:Type, as:T*. null(as)
T:Type, as:T*. null(as) ![]()
![]()
![]()
![]()
![]() T:Type, as,bs:T*. (as @ bs)
T:Type, as,bs:T*. (as @ bs) ![]() T*
T*![]() A:Type, B:(A
A:Type, B:(A![]()
![]() Type), p:a:A
Type), p:a:A![]() B(a). 2of(p)
B(a). 2of(p) ![]() B(1of(p))
B(1of(p))