| 1 | 18. j if null(nil) if null(nil) 0 ;1= 0 ;1= hd(nil) hd(nil) 1+||1:tl(nil)|| else ||1:tl(nil)|| fi
+i 1+||1:tl(nil)|| else ||1:tl(nil)|| fi
+i (1+if null(nil) (1+if null(nil) 0 ;1= 0 ;1= hd(nil) hd(nil) 1+||1:tl(nil)|| else ||1:tl(nil)|| fi)
=
k 1+||1:tl(nil)|| else ||1:tl(nil)|| fi)
=
k if null(nil) if null(nil) 0 ;1= 0 ;1= hd(nil) hd(nil) 1+||1:tl(nil)|| else ||1:tl(nil)|| fi
+k 1+||1:tl(nil)|| else ||1:tl(nil)|| fi
+k (1+if null(nil) (1+if null(nil) 0 ;1= 0 ;1= hd(nil) hd(nil) 1+||1:tl(nil)|| else ||1:tl(nil)|| fi) 1+||1:tl(nil)|| else ||1:tl(nil)|| fi)
19. ||1:([0]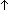 j)||+||1:([1] j)||+||1:([1]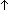 i)|| i)||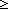 0 0
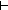 False False |