| 1 | 5. Fin(Alph)
6. Fin(St)
7. EquivRel x,y:Alph*. x LangOf(Auto)-induced Equiv y
8. h: Alph* 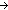 Alph* Alph*
9.  x,y:Alph*. x = y x,y:Alph*. x = y 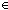 x,y:Alph*//(x LangOf(Auto)-induced Equiv y) x,y:Alph*//(x LangOf(Auto)-induced Equiv y) 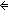  h(x) = h(y) h(x) = h(y)
10.  x:Alph*. x = h(x) x:Alph*. x = h(x) 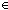 x,y:Alph*//(x LangOf(Auto)-induced Equiv y) x,y:Alph*//(x LangOf(Auto)-induced Equiv y)
11. b1: Alph*
12. b2: Alph*
13. b1 LangOf(Auto)-induced Equiv b2
14. (Result(Auto)c(Result(Auto)h(b1))) = (Result(Auto)h(b1))
15. b1 = b2 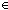 x,y:Alph*//(x LangOf(Auto)-induced Equiv y) x,y:Alph*//(x LangOf(Auto)-induced Equiv y) 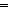  h(b1) = h(b2) h(b1) = h(b2)
16. (b1 = b2 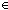 x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) x,y:Alph*//(x LangOf(Auto)-induced Equiv y)) 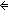 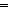 (h(b1) = h(b2)) (h(b1) = h(b2))
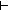 b1 = b2 b1 = b2 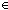 x,y:Alph*//(x LangOf(Auto)-induced Equiv y) x,y:Alph*//(x LangOf(Auto)-induced Equiv y) |