| assert |
Def 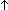 b == if b b == if b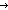 True else False fi True else False fi
Thm*  b: b: . b . b 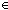 Prop Prop
|
| equiv_rel |
Def EquivRel x,y:T. E(x;y)
== Refl(T;x,y.E(x;y)) & Sym x,y:T. E(x;y) & Trans x,y:T. E(x;y)
Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). (EquivRel x,y:T. E(x,y)) Prop). (EquivRel x,y:T. E(x,y)) 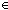 Prop Prop
|
| min_el |
Def Min{ x | xEn } == MinArg(E(n) : {0..n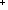 }) })
Thm*  E:( E:(       ), n: ), n: . Min{ x | xEn } . Min{ x | xEn } 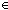 
|
| nat |
Def  == {i: == {i: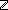 | 0 | 0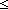 i } i }
Thm*  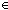 Type Type
|
| rev_implies |
Def P 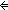 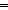 Q == Q Q == Q 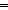 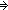 P P
Thm*  A,B:Prop. (A A,B:Prop. (A 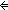 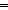 B) B) 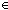 Prop Prop
|
| trans |
Def Trans x,y:T. E(x;y) ==  a,b,c:T. E(a;b) a,b,c:T. E(a;b) 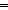 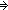 E(b;c) E(b;c) 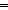 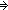 E(a;c) E(a;c)
Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Trans x,y:T. E(x,y) Prop). Trans x,y:T. E(x,y) 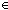 Prop Prop
|
| sym |
Def Sym x,y:T. E(x;y) ==  a,b:T. E(a;b) a,b:T. E(a;b) 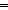 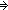 E(b;a) E(b;a)
Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Sym x,y:T. E(x,y) Prop). Sym x,y:T. E(x,y) 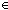 Prop Prop
|
| refl |
Def Refl(T;x,y.E(x;y)) ==  a:T. E(a;a) a:T. E(a;a)
Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Refl(T;x,y.E(x,y)) Prop). Refl(T;x,y.E(x,y)) 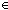 Prop Prop
|
| min_arg |
Def MinArg(f : {0..n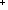 }) == n-MinAr(f;n;n) }) == n-MinAr(f;n;n)
Thm*  f:( f:(    ), n: ), n: . MinArg(f : {0..n . MinArg(f : {0..n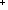 }) }) 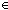  (n+1) (n+1)
|
| le |
Def A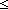 B == B == 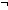 B < A B < A
Thm*  i,j: i,j: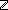 . i . i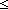 j j 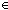 Prop Prop
|
| min_ar |
Def MinAr(f;i;n) == if (f(n-i))=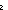 (f(n)) (f(n))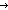 i else MinAr(f;i-1;n) fi (recursive) i else MinAr(f;i-1;n) fi (recursive)
Thm*  f:( f:(    ), n: ), n: , i: , i: (n+1). MinAr(f;i;n) (n+1). MinAr(f;i;n) 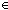  (i+1) (i+1)
|
| not |
Def 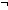 A == A A == A 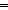 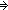 False False
Thm*  A:Prop. ( A:Prop. (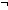 A) A) 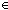 Prop Prop
|
| eq_bool |
Def p=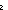 q == (p q == (p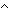 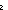 q) q) 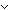 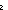 ( (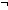 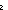 p p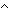 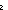 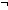 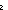 q) q)
Thm*  p,q: p,q: . p= . p=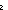 q q 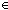 
|
| bnot |
Def 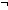 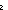 b == if b b == if b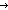 false false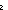 else true else true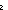 fi fi
Thm*  b: b: . . 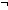 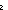 b b 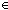 
|
| band |
Def p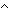 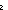 q == if p q == if p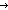 q else false q else false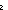 fi fi
Thm*  p,q: p,q: . (p . (p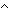 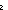 q) q) 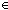 
|
| bor |
Def p 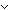 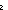 q == if p q == if p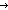 true true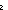 else q fi else q fi
Thm*  p,q: p,q: . (p . (p 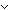 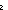 q) q) 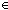 
|
![]() b:
b:![]() . b
. b ![]() Prop
Prop![]() T:Type, E:(T
T:Type, E:(T![]()
![]() T
T![]()
![]() Prop). (EquivRel x,y:T. E(x,y))
Prop). (EquivRel x,y:T. E(x,y)) ![]() Prop
Prop![]() E:(
E:(![]()
![]()
![]()
![]()
![]()
![]()
![]() ), n:
), n:![]() . Min{ x | xEn }
. Min{ x | xEn } ![]()
![]()
![]()
![]() Type
Type![]() A,B:Prop. (A
A,B:Prop. (A ![]()
![]() B)
B) ![]() Prop
Prop![]() T:Type, E:(T
T:Type, E:(T![]()
![]() T
T![]()
![]() Prop). Trans x,y:T. E(x,y)
Prop). Trans x,y:T. E(x,y) ![]() Prop
Prop![]() T:Type, E:(T
T:Type, E:(T![]()
![]() T
T![]()
![]() Prop). Sym x,y:T. E(x,y)
Prop). Sym x,y:T. E(x,y) ![]() Prop
Prop![]() T:Type, E:(T
T:Type, E:(T![]()
![]() T
T![]()
![]() Prop). Refl(T;x,y.E(x,y))
Prop). Refl(T;x,y.E(x,y)) ![]() Prop
Prop![]() f:(
f:(![]()
![]()
![]()
![]() ), n:
), n:![]() . MinArg(f : {0..n
. MinArg(f : {0..n![]() })
}) ![]()
![]() (n+1)
(n+1)![]() i,j:
i,j:![]() . i
. i![]() j
j ![]() Prop
Prop![]() f:(
f:(![]()
![]()
![]()
![]() ), n:
), n:![]() , i:
, i:![]() (n+1). MinAr(f;i;n)
(n+1). MinAr(f;i;n) ![]()
![]() (i+1)
(i+1)![]() A:Prop. (
A:Prop. (![]() A)
A) ![]() Prop
Prop![]() p,q:
p,q:![]() . p=
. p=![]() q
q ![]()
![]()
![]() b:
b:![]() .
. ![]()
![]() b
b ![]()
![]()
![]() p,q:
p,q:![]() . (p
. (p![]()
![]() q)
q) ![]()
![]()
![]() p,q:
p,q:![]() . (p
. (p ![]()
![]() q)
q) ![]()
![]()