At: reach lemma 1 1 2 2 2 1 1 1
1. Alph: Type
2. S: ActionSet(Alph)
3. si: S.car
4. nn: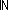 
5. f: 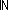nn
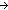Alph
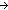
6. g: Alph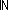nn
7. Fin(S.car)
8. InvFuns(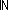nn; Alph; f; g)
9. k: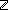 
10. 0 < k
11. k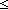
nn
12. RLa: S.car*
13. 
i:{1..1
}, a:Alph. si = S.act(a,[si][i]) 
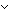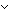False mem_f(S.car;S.act(a,[si][i]);RLa)
14. a:Alph. g(a) < k-1 
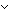si = S.act(a,si) False 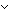mem_f(S.car;S.act(a,si);RLa)
15. s:S.car. mem_f(S.car;s;RLa) (
w:Alph*. (S:w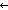
si) = s)
16. a: Alph
17. g(a) < k
18. g(a) < k-1
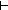si = S.act(a,si) 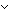False 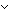S.act(f(k-1),si) = S.act(a,si) 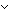mem_f(S.car;S.act(a,si);RLa)
By:
FwdThru 14 [-1]
THEN
ProveProp
Generated subgoals:None
About:
