DiscreteMath Sections DiscrMathExt Doc
IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html
Def  A == A  False

is mentioned by

Thm*  Dedekind-Infinite(A)  Finite(A)[dedekind_imp_nonfin]
Thm*  InvFuns(;{xy:()| xy = <0,0>   };next_nat_pair;prev_nat_pair)[next_nat_pair_vs_prev_nat_pair]
Thm*  prev_nat_pair  {xy:()| xy = <0,0>   }[prev_nat_pair_wf]
Thm*  xy:(). <0,0> = next_nat_pair(xy)  [next_nat_pair_not_zeroes]
Thm*  (x:A. Dec(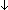P(x)))  (A ~ ({x:A| P(x) }+{x:A| P(x) }))[card_split_decbl_squash]
Thm*  B:(AType), P:(AProp).
Thm*  (i:A. Dec(P(i)))
Thm*  
Thm*  ((i:AB(i)) ~ ((i:{i:A| P(i) }B(i))+(i:{i:A| P(i) }B(i))))		[card_split_sigma_dom_decbl]
Thm*  (x:A. Dec(P(x)))  (A ~ ({x:A| P(x) }+{x:A| P(x) }))[card_split_decbl]
Thm*  Finite()[nat_not_finite]
Thm*  (() ~ )[not_nat_occ_natfuns]
Thm*  (A:Type. Finite(A)  Infinite(A))  (D:Type. (D)  (D))[absurd_nonfinite_imp_infinite]
Thm*  (A:Type. Finite(A)  Unbounded(A))  (P:Prop. P  P)[nonfin_eqv_unb_inf_iff_negnegelim]
Thm*  (A:Type. Finite(A)  Unbounded(A))  (D:Type. (D)  (D))[absurd_nonfin_imp_unb_inf]
Thm*  k:. Infinite(k)[nsub_not_infinite]
Thm*  (P:Prop. P  P)  (A:Type. Finite(A)  Unbounded(A))[negnegelim_imp_notfin_imp_unb_inf]
Thm*  Infinite(A)  Finite(A)[infinite_imp_nonfinite]
Thm*  Unbounded(A)  Finite(A)[unb_inf_not_fin]
Thm*  (x:A. Dec(P(x)))
Thm*  
Thm*  ((x:AB(x)) ~ ((x:A st P(x)B(x))(x:A st P(x)B(x))))		[card_split_prod_intseg_family_decbl]
Thm*  P:{P:(Prop)| i:. P(i) }. 
Thm*  (i:. Dec(P(i)))  ({i:| P(i) & (j:. j<i  P(j)) })		[least_exists2]
Thm*  k:, P:{P:(kProp)| i:k. P(i) }.
Thm*  (i:k. Dec(P(i)))  ({i:k| P(i) & (j:i. P(j)) })		[least_exists]
Thm*  Dec(P)  (!i:2. if i=0 P else P fi)[decidable_vs_unique_nsub2]
Thm*  (A ~ 0)  (A)[card0_iff_uninhabited]
Thm*  k:, j:k. {i:k| i = j } ~ (k-1)[nsub_delete_rw]
Thm*  k:, j:k, m:. m = k-1  ({i:k| i = j } ~ m)[nsub_delete]
Thm*  (A:Type, R:(AAProp).
Thm*  ((A) & (Trans x,y:A. R(x;y)) & (x:A. y:A. R(x;y))
Thm*  (& (x:A. R(x;x))
Thm*  (& Finite(A))		[no_finite_model]
Thm*  p:{p:()| i:. p(i) }, j:(least i:. p(i)). p(j)[least_is_least2]
Thm*  k:, p:{p:(k)| i:k. p(i) }, j:(least i:. p(i)). p(j)[least_is_least]
Thm*  p:{p:()| i:. p(i) }. 
Thm*  (least i:. p(i))  {i:| p(i) & (j:. j<i  p(j)) }		[least_characterized2]
Thm*  k:, p:{p:(k)| i:k. p(i) }.
Thm*  (least i:. p(i))  {i:k| p(i) & (j:i. p(j)) }		[least_characterized]
Thm*  m:, f:(m). Inj(m; ; f)  (x:m, y:x. f(x) = f(y))[finite_inj_counter_example]
Thm*  Inj((m+1); (k+1); f)
Thm*  
Thm*  (i:m. f(i) = k  (Replace value k by f(m) in f)(i) = f(i) k)		[delete_fenum_value_comp2]
Thm*  Bij({u:| P(u) }; {v:| Q(v) }; f)
Thm*  
Thm*  (m:{u:| P(u) }, k:{v:| Q(v) }.
Thm*  (Bij({u:| P(u) & u = m }; {v:| Q(v) & v = k };
Thm*  (Bij(Replace value k by f(m) in f))		[delete_fenum_value_is_fenum_gen]
Thm*  Inj({u:| P(u) }; {v:| Q(v) }; f)
Thm*  
Thm*  (m:{u:| P(u) }, k:{v:| Q(v) }.
Thm*  (Inj({u:| P(u) & u = m }; {v:| Q(v) & v = k };
Thm*  (Inj(Replace value k by f(m) in f))		[delete_fenum_value_is_inj_gen]
Thm*  Inj({u:| P(u) }; {v:| Q(v) }; f)
Thm*  
Thm*  (m:{u:| P(u) }, k:{v:| Q(v) }.
Thm*  ((Replace value k by f(m) in f)
Thm*  ( {u:| P(u) & u = m }{v:| Q(v) & v = k }
Thm*  (& Inj({u:| P(u) & u = m }; {v:| Q(v) & v = k };
Thm*  (& Inj(Replace value k by f(m) in f))		[delete_fenum_value_is_inj_genW]
Thm*  Inj({u:| P(u) }; {u:| Q(u) }; f)
Thm*  
Thm*  (m:{u:| P(u) }, k:{v:| Q(v) }, i:{u:| P(u) & u = m }.
Thm*  (f(i) = k
Thm*  (
Thm*  ((Replace value k by f(m) in f)(i) = f(i)  {v:| Q(v) & v = k })		[delete_fenum_value_comp2_gen]
Thm*  Inj({u:| P(u) }; {u:| Q(u) }; f)
Thm*  
Thm*  (m:{u:| P(u) }, k:{v:| Q(v) }, i:{u:| P(u) & u = m }.
Thm*  (f(i) = k
Thm*  (
Thm*  ((Replace value k by f(m) in f)(i) = f(m)  {v:| Q(v) & v = k })		[delete_fenum_value_comp1_gen]
Thm*  Inj({k:| P(k) }; {k:| Q(k) }; f)
Thm*  
Thm*  (m:{u:| P(u) }, k:{v:| Q(v) }.
Thm*  ((Replace value k by f(m) in f)
Thm*  ( {u:| P(u) & u = m }{v:| Q(v) & v = k })		[delete_fenum_value_wf_gen]
Thm*  a:, b:, j:b, f:((a-1) inj {x:b| x = j }).
Thm*  (i.if i=a-1 j else f(i) fi)  a inj b		[nsub_inj_fill_typing]
Thm*  a:, b:, f:(a inj b). f  (a-1) inj {x:b| x = f(a-1) }[nsub_inj_lop_typing]
Thm*  (A)  (!(A inj B))[inj_from_empty_unique]
Thm*  f:(A inj B), a:A. f  {x:A| x = a } inj {y:B| y = f(a) }[inj_point_deletion_inj]
Thm*  f:(A inj B), a:A. f  {x:A| x = a }{y:B| y = f(a) }[inj_point_deletion]
Def  Dedekind-Infinite(A) == a:A, f:(AA). Inj(A; A; f) & (x:A. f(x) = a)[Dedekind_infinite]

In prior sections: core bool 1 rel 1 LogicSupplement int 2 num thy 1 SimpleMulFacts IteratedBinops

Try larger context: DiscrMathExt IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html

DiscreteMath Sections DiscrMathExt Doc