Def  A ~ B == f:(AB), g:(BA). InvFuns(A;B;f;g)

is mentioned by

Thm*  (AH ~ 8)  ((AH{1...8}) ~ 64)	[chessboard_example]
Thm*  p:(a {k} ). {i:a| p(i) } ~ k	[card_st_sized_bool]
Thm*  p:(a). {x:a| p(x) } ~ (size(a)(p))	[card_st_vs_boolsize]
Thm*  f:(a2).  Thm*  (i:a. P(i)  f(i) = 1  2)  ({x:a| P(x) } ~ (Msize(f)))	[card_st_vs_msize]
Thm*  (a {k} ) ~ (a {k} 2)	[card_boolset_vs_mset]
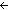Thm*  (a bij a) ~ (aa)	[nsub_bij_ooc_invpair]
Thm*  (k inj k) ~ (k onto k)	[nsub_inj_ooc_nsub_surj]
Thm*  (k inj k) ~ (k bij k)	[nsub_inj_ooc_nsub_bij]
Thm*  (k onto k) ~ (k bij k)	[nsub_surj_ooc_nsub_bij]
Thm*  (k:k) ~	[card_nat_vs_nat_tuples_all]
Thm*  (k:k) ~	[card_nat_vs_nat_tuples]
Thm*  k:. (k) ~	[card_nat_vs_nat_tuple]
Thm*  () ~	[card_nat_vs_nat_nat]
Thm*  ((A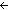B)) ~ (A ~ B)	[inv_pair_inv2]
Thm*  (A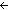B) ~ (A ~ B)	[inv_pair_inv]
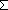Thm*  a:, b:(a). (i:ab(i)) ~ ( i:a. b(i))	[card_sigma_vs_nsub_sigma]
Thm*  a,b:. (a+b) ~ (a+b)	[nsub_add_rw]
Thm*  (ABC) ~ (BAC)	[card_curry_simple2]
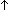Thm*  a,b:. (ab) ~ (ba)	[card_fun_vs_nsub_exp]
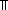Thm*  a:, b:(a). (i:ab(i)) ~ ( i:a. b(i))	[card_pi_vs_nsub_pi]
Thm*  (k inj k) ~ (k!)	[nsub_inj_factorial]
Thm*  (a inj b) ~ (b!a)	[nsub_inj_factorial_tail]
Thm*  (b inj b) ~ (b!)	[nsub_inj_factorial2]
Thm*  a,b:. (A ~ a)  (B ~ b)  ((AB) ~ (ab))	[finite_indep_sum_card]
Thm*  a,b:. (ab) ~ (ab)	[nsub_mul_rw]
Thm*  a,b,c:. ab = c  ((ab) ~ c)	[nsub_mul]
Thm*  c,a,b:. a+b = c    ((a+b) ~ c)	[nsub_add]
Thm*  a,b:, c:{a...b}. ({a..c}+{c..b}) ~ {a..b}	[intseg_split]
Thm*  a,b:. {a...b} ~ (1+b-a)	[nsub_intiseg_rw]
Thm*  a:, b:. {a...b} ~ {a..(b+1)}	[intiseg_intseg_plus]
Thm*  a,b',b:. b = b'+1  ({a...b'} ~ {a..b})	[intiseg_intseg]
Thm*  a,b:. {a..b} ~ (b-a)	[nsub_intseg_rw]
Thm*  c,a:, b:. c = b-a  ({a..b} ~ c)	[nsub_intseg]
Thm*   ~ 2	[nsub_bool]
Thm*  Unit ~ 1	[nsub_unit]
Thm*  a:, b,c:. {a..b} ~ {(a+c)..(b+c)}	[intseg_shift_by]
Thm*  a,b,a',b':. b-a = b'-a'  ({a..b} ~ {a'..b'})	[intseg_shift]
Thm*  Void ~ 0	[nsub_void]
Thm*  a,b:. ba  (Void ~ {a..b})	[intseg_void]
Thm*  (xy:(x:AB(x))C(xy)) ~ (x:Ay:B(x)C(<x,y>))	[card_sigma_distr]
Thm*  (z:(x:AB(x))C(z)) ~ (x:Ay:B(x)C(<x,y>))	[card_curry]
Thm*  (ABC) ~ (ABC)	[card_curry_simple]
Thm*  (A ~ A')  (B ~ B')  ((AB) ~ (A'B'))	[function_functionality_wrt_one_one_corr]
Thm*  B,B':(AType). (x:A. B(x) ~ B'(x))  ((x:AB(x)) ~ (x:AB'(x)))	[function_functionality_wrt_one_one_corr_B]
Thm*  (x:A. B(x)) ~ (x:A'. B'(x))  ((x:AB(x)) ~ (x:A'B'(x)))	[card_pi]
Thm*  a,b:, B:({a..b}Type). Thm*  a<b  ((i:{a..b}B(i)) ~ ((i:{a..(b-1)}B(i))+B(b-1)))	[card_split_end_sum_intseg_family]
Thm*  a,b:, c:{a...b}, B:({a..b}Type). Thm*  (i:{a..b}B(i)) ~ ((i:{a..c}B(i))+(i:{c..b}B(i)))	[card_split_sum_intseg_family]
Thm*  (x:A. Dec(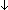P(x)))  (A ~ ({x:A| P(x) }+{x:A| P(x) }))	[card_split_decbl_squash]
Thm*  (A+0) ~ A	[card_nsub0_union_2]
Thm*  (0+A) ~ A	[card_nsub0_union]
Thm*  B:(AType), P:(AProp). Thm*  (i:A. Dec(P(i))) Thm*   Thm*  ((i:AB(i)) ~ ((i:{i:A| P(i) }B(i))+(i:{i:A| P(i) }B(i))))	[card_split_sigma_dom_decbl]
Thm*  B:(AType), P:(AProp). Thm*  (i:{i:A| P(i) }B(i)) ~ {v:(i:AB(i))| P(v/x,y. x) }	[card_sigma_st_dom]
Thm*  (x:A. Dec(P(x)))  (A ~ ({x:A| P(x) }+{x:A| P(x) }))	[card_split_decbl]
Thm*  (A+B) ~ (i:2if i=0 A else B fi)	[card_union_vs_sigma]
Thm*  (A+B) ~ (B+A)	[card_union_swap]
Thm*  a,b:, c:{a...b}, B:({a..b}Type). Thm*  (i:{a..b}B(i)) ~ ((i:{a..c}B(i))(i:{c..b}B(i)))	[card_split_prod_intseg_family]
Thm*  (A ~ A')  (B ~ B')  ((AB) ~ (A'B'))	[product_functionality_wrt_one_one_corr]
Thm*  (q:A/E{x:A| q = x  A/E }) ~ A	[card_quotient]
Thm*  B,B':(AType). (x:A. B(x) ~ B'(x))  ((x:AB(x)) ~ (x:AB'(x)))	[product_functionality_wrt_one_one_corr_B]
Thm*  (x:A. B(x)) ~ (x:A'. B'(x))  ((x:AB(x)) ~ (x:A'B'(x)))	[card_sigma]
Thm*  (x:A. 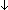B(x)  B'(x))  ({x:A| B(x) } ~ {x:A| B'(x) })	[set_functionality_wrt_one_one_corr_n_pred]
Thm*  (x:A. B(x)  B'(x))  ({x:A| B(x) } ~ {x:A| B'(x) })	[set_functionality_wrt_one_one_corr_n_pred2]
Thm*  Bij(A; A'; f) Thm*   Thm*  (x:A. B(x)  B'(f(x)))  ({x:A| B(x) } ~ {x:A'| B'(x) })	[card_settype_sq]
Thm*  Bij(A; A'; f) Thm*   Thm*  (x:A. B(x)  B'(f(x)))  ({x:A| B(x) } ~ {x:A'| B'(x) })	[card_settype]
Thm*  (AB) ~ (BA)	[card_product_swap]
Thm*  (A ~ A')  (B ~ B')  ((A+B) ~ (A'+B'))	[union_functionality_wrt_one_one_corr]
Thm*  (A ~ A')  (B ~ B')  (:A. B) ~ (:A'. B')	[one_one_corr_fams_indep_if_one_one_corr]
Thm*  (x:A. B(x) ~ B'(x))  (x:A. B(x)) ~ (x:A. B'(x))	[one_one_corr_fams_if_one_one_corr_B]
Thm*  P:(ABProp). (x:A. !y:B. P(x;y))  (A ~ (y:B{x:A| P(x;y) }))	[partition_type]
Thm*  a,b:. (a ~ b)  a = b	[fin_card_vs_nat_eq]
Thm*  (A ~ m)  (A ~ k)  m = k	[counting_is_unique]
Thm*  (() ~ )	[not_nat_occ_natfuns]
Thm*  (f:(AB). Bij(A; B; f))  (B ~ A)	[bij_iff_1_1_corr_version2a]
Thm*  (A ~ B)  Infinite(A)  Infinite(B)	[ooc_preserves_infiniteness]
Thm*  (A ~ B)  Unbounded(A)  Unbounded(B)	[ooc_preserves_unb_inf]
Thm*   ~	[int_ooc_nat]
Thm*  (f:(AB). Bij(A; B; f))  (A ~ B)	[bij_iff_1_1_corr_version2]
Thm*  (A ~ B)  (B ~ C)  (A ~ C)	[one_one_corr_2_transitivity]
Thm*  (A ~ B)  (B ~ A)	[one_one_corr_2_inversion]
Thm*  A ~ A	[one_one_corr_2_reflex]
Thm*  (A ~ A')  (B ~ B')  ((A ~ B)  (A' ~ B'))	[one_one_corr_2_functionality_wrt_one_one_corr]
Thm*  (A ~ B)  ((A)  (B))	[inhabited_functionality_wrt_one_one_corr]
Thm*  (A ~ B)  (A  B)	[iff_weakening_wrt_one_one_corr_2]
Thm*  EquivRel X,Y:Type. X ~ Y	[one_one_corr_is_equiv_rel]
Thm*  (A ~ A')  (B ~ B')  ((A inj B) ~ (A' inj B'))	[injection_type_functionality_wrt_ooc]
Thm*  (A ~ B)  Dedekind-Infinite(A)  Dedekind-Infinite(B)	[ooc_preserves_dededkind_inf]
Thm*  (A ~ A')  (B ~ B')  ((A onto B) ~ (A' onto B'))	[surjection_type_functionality_wrt_ooc]
Thm*  (x:A. Dec(P(x))) Thm*   Thm*  ((x:AB(x)) ~ ((x:A st P(x)B(x))(x:A st P(x)B(x))))	[card_split_prod_intseg_family_decbl]
Thm*  A:Type, B:Type. (A ~~ B)  (A ~ B)	[one_one_corr_iff_one_one_corr_2]
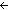Thm*  (A ~ A')  (B ~ B')  ((AB) ~ (A'B'))	[inv_pair_functionality_wrt_one_one_corr]
Thm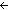*  ((AB))  (A ~ B)	[inv_pair_iff_ooc]
Thm*  a,a':. a'-a = 1  (B:({a..a'}Type). (i:{a..a'}B(i)) ~ B(a))	[card_sum_family_intseg_singleton_elim]
Thm*  B:({a:A}Type). (i:{a:A}B(i)) ~ B(a)	[card_sum_family_singleton_elim]
Thm*  (A ~ 0)  (A)	[card0_iff_uninhabited]
Thm*  A = B  (A ~ B)	[one_one_corr_2_weakening_wrt]
Thm*  {x:A| 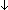B(x) } ~ {x:A| B(x) }	[subset_sq_remove_card]
Thm*  a,a':. a'-a = 1  (B:({a..a'}Type). (i:{a..a'}B(i)) ~ B(a))	[card_prod_family_intseg_singleton_elim]
Thm*  (i:{a:A}B(i)) ~ B(a)	[card_prod_family_singleton_elim]
Thm*  a,b:. (a inj b) ~ (b((a-1) inj (b-1)))	[card_nsub_inj_vs_lopped]
Thm*  k:, j:k. {i:k| i = j } ~ (k-1)	[nsub_delete_rw]
Thm*  k:, j:k, m:. m = k-1  ({i:k| i = j } ~ m)	[nsub_delete]
Thm*  (0A) ~ 1	[card_void_dom_fun_unit]
Thm*  (A ~ 1)  (!A)	[card1_iff_inhabited_uniquely]
Thm*  a,a':. Thm*  a'-a = 1  (B:({a..a'}Type). (i:{a..a'}B(i)) ~ ({a:}B(a)))	[card_sum_family_singleton_vs_intseg]
Thm*  {x:{x:A| P(x) }| Q(x) } ~ {x:A| P(x) & Q(x) }	[card_subset_vs_and]
Thm*  {x:A| if b P(x) else Q(x) fi } ~ if b {x:A| P(x) } else {x:A| Q(x) } fi	[ifthenelse_distr_subtype_ooc]
Thm*  (A bij B) ~ ((A inj B)(A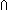 onto B))	[bijtype_ooc_inj_isect_surjtype]
Thm*  (ABC) ~ ((AB)C)	[simple_card_cross_assoc]
Thm*  (A ~ B)  Finite(A)  Finite(B)	[ooc_preserves_finiteness]
Thm*   ~	[nat_plus_ooc_nat]
Thm*  k:. (k+) ~	[fin_plus_nat_ooc_nat]
Thm*  A = A'  B = B'  (A ~ B) = (A' ~ B')	[one_one_corr_2_functionality_wrt_eq]
Def  Finite(A) == n:. A ~ n	[is_finite_type]

Try larger context: DiscrMathExt IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html