| 1 |
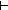 ( ( f.<f(a-1),f>) f.<f(a-1),f>)  ( ( a inj a inj  b) b)  (i: (i: b b  (a-1) inj (a-1) inj {x: {x: b| b|  x = i }) x = i })
 | 3 steps |
| 2 |
3. ( f.<f(a-1),f>) f.<f(a-1),f>)  ( ( a inj a inj  b) b)  (i: (i: b b  (a-1) inj (a-1) inj {x: {x: b| b|  x = i }) x = i })
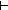 ( ( ie.ie/i,e. ie.ie/i,e.  x.if x= x.if x= a-1 a-1 i else e(x) fi) i else e(x) fi)
  (i: (i: b b  (a-1) inj (a-1) inj {x: {x: b| b|  x = i }) x = i })   a inj a inj  b b
 | 2 steps |
| 3 |
3. ( f.<f(a-1),f>) f.<f(a-1),f>)  ( ( a inj a inj  b) b)  (i: (i: b b  (a-1) inj (a-1) inj {x: {x: b| b|  x = i }) x = i })
4. ( ie.ie/i,e. ie.ie/i,e.  x.if x= x.if x= a-1 a-1 i else e(x) fi) i else e(x) fi)
4.  (i: (i: b b  (a-1) inj (a-1) inj {x: {x: b| b|  x = i }) x = i })   a inj a inj  b b
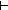 InvFuns( InvFuns( a inj a inj  b;i: b;i: b b  (a-1) inj (a-1) inj {x: {x: b| b|  x = i } x = i }
 InvFuns; InvFuns; f.<f(a-1),f>; f.<f(a-1),f>; ie.ie/i,e. ie.ie/i,e.  x.if x= x.if x= a-1 a-1 i else e(x) fi) i else e(x) fi)
 | 22 steps |