| enum |
Def enum(l) == 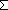 (q (q ||l|| ||l|| )+en(l) )+en(l)
Thm*  q: q: , l: , l: q*. enum(l) q*. enum(l)  
|
| int_seg |
Def {i..j } == {k: } == {k: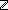 | i | i 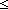 k < j } k < j }
Thm*  m,n: m,n: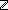 . {m..n . {m..n } }  Type Type
|
| nat |
Def  == {i: == {i: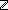 | 0 | 0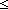 i } i }
Thm*   Type Type
|
| en |
Def en(l) == if null(l)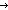 0 else hd(l)+en(tl(l)) 0 else hd(l)+en(tl(l)) n fi (recursive) n fi (recursive)
Thm*  n: n: , l: , l: n*. en(l) n*. en(l)  
|
| length |
Def ||as|| == Case of as; nil 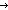 0 ; a.as' 0 ; a.as' 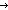 ||as'||+1 (recursive) ||as'||+1 (recursive)
Thm*  A:Type, l:A*. ||l|| A:Type, l:A*. ||l||  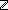
Thm* ||nil||  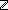
|
| geom_series |
Def 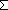 (q (q n n ) == if n= ) == if n=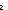 0 0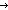 0 else 0 else 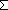 (q (q n-1 n-1 )+(q )+(q n-1) fi (recursive) n-1) fi (recursive)
Thm*  q,n: q,n: . . 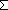 (q (q n n ) )  
|
| lelt |
Def i 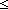 j < k == i j < k == i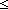 j & j < k j & j < k
|
| le |
Def A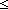 B == B == 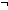 B < A B < A
Thm*  i,j: i,j: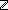 . i . i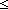 j j  Prop Prop
|
| tl |
Def tl(l) == Case of l; nil 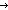 nil ; h.t nil ; h.t 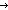 t t
Thm*  A:Type, l:A*. tl(l) A:Type, l:A*. tl(l)  A* A*
|
| hd |
Def hd(l) == Case of l; nil 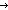 "?" ; h.t "?" ; h.t 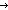 h h
Thm*  A:Type, l:A*. ||l|| A:Type, l:A*. ||l||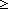 1 1   hd(l) hd(l)  A A
|
| null |
Def null(as) == Case of as; nil 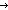 true true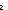 ; a.as' ; a.as' 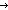 false false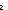
Thm*  T:Type, as:T*. null(as) T:Type, as:T*. null(as)  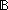
Thm* null(nil)  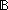
|
| exp |
Def (base power) == if power= power) == if power=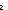 0 0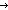 1 else base 1 else base (base (base power-1) fi (recursive) power-1) fi (recursive)
Thm*  n,k: n,k: . (n . (n k) k)  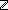
Thm*  n,k: n,k: . (n . (n k) k)  
|
| eq_int |
Def i=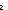 j == if i=j j == if i=j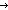 true true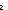 ; false ; false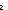 fi fi
Thm*  i,j: i,j: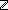 . i= . i=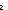 j j  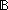
|
| not |
Def 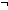 A == A A == A   False False
Thm*  A:Prop. ( A:Prop. (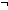 A) A)  Prop Prop
|
![]() q:
q:![]() , l:
, l:![]() q*. enum(l)
q*. enum(l) ![]()
![]()
![]() m,n:
m,n:![]() . {m..n
. {m..n![]() }
} ![]() Type
Type![]()
![]() Type
Type![]() n:
n:![]() , l:
, l:![]() n*. en(l)
n*. en(l) ![]()
![]()
![]() A:Type, l:A*. ||l||
A:Type, l:A*. ||l|| ![]()
![]()
![]()
![]()
![]() q,n:
q,n:![]() .
. ![]() (q
(q![]() n
n![]() )
) ![]()
![]()
![]() i,j:
i,j:![]() . i
. i![]() j
j ![]() Prop
Prop![]() A:Type, l:A*. tl(l)
A:Type, l:A*. tl(l) ![]() A*
A*![]() A:Type, l:A*. ||l||
A:Type, l:A*. ||l||![]() 1
1 ![]()
![]() hd(l)
hd(l) ![]() A
A![]() T:Type, as:T*. null(as)
T:Type, as:T*. null(as) ![]()
![]()
![]()
![]()
![]() n,k:
n,k:![]() . (n
. (n![]() k)
k) ![]()
![]()
![]() n,k:
n,k:![]() . (n
. (n![]() k)
k) ![]()
![]()
![]() i,j:
i,j:![]() . i=
. i=![]() j
j ![]()
![]()
![]() A:Prop. (
A:Prop. (![]() A)
A) ![]() Prop
Prop