Thm*  L:(A+B) List, a:A. mapoutl(L) = [a] L:(A+B) List, a:A. mapoutl(L) = [a]   ( ( L1,L2:(A+B) List. L = (L1 @ [inl(a)] @ L2) & mapoutl(L1) = nil & mapoutl(L2) = nil) L1,L2:(A+B) List. L = (L1 @ [inl(a)] @ L2) & mapoutl(L1) = nil & mapoutl(L2) = nil) | [mapoutl_is_singleton] |
Thm*  L:(A+B) List, l1,l2:A List. mapoutl(L) = (l1 @ l2) L:(A+B) List, l1,l2:A List. mapoutl(L) = (l1 @ l2)   ( ( L1,L2:(A+B) List. L = (L1 @ L2) & mapoutl(L1) = l1 & mapoutl(L2) = l2) L1,L2:(A+B) List. L = (L1 @ L2) & mapoutl(L1) = l1 & mapoutl(L2) = l2) | [mapoutl_is_append] |
Thm*  L1,L2:(A+B) List. mapoutl(L1 @ L2) ~ (mapoutl(L1) @ mapoutl(L2)) L1,L2:(A+B) List. mapoutl(L1 @ L2) ~ (mapoutl(L1) @ mapoutl(L2)) | [mapoutl_append] |
Thm*  l1,l2:T List. no_repeats(T;l1 @ l2) l1,l2:T List. no_repeats(T;l1 @ l2)   l_disjoint(T;l1;l2) & no_repeats(T;l1) & no_repeats(T;l2) l_disjoint(T;l1;l2) & no_repeats(T;l1) & no_repeats(T;l2) | [no_repeats_append_iff] |
Thm*  a,b,c:T List. l_disjoint(T;c;a @ b) a,b,c:T List. l_disjoint(T;c;a @ b)   l_disjoint(T;c;a) & l_disjoint(T;c;b) l_disjoint(T;c;a) & l_disjoint(T;c;b) | [l_disjoint_append2] |
Thm*  a,b,c:T List. l_disjoint(T;a @ b;c) a,b,c:T List. l_disjoint(T;a @ b;c)   l_disjoint(T;a;c) & l_disjoint(T;b;c) l_disjoint(T;a;c) & l_disjoint(T;b;c) | [l_disjoint_append] |
Thm*  L:T List, x,y:T. x before y L:T List, x,y:T. x before y  L L   ( ( L1,L2,L3:T List. L = (L1 @ [x] @ L2 @ [y] @ L3)) L1,L2,L3:T List. L = (L1 @ [x] @ L2 @ [y] @ L3)) | [l_before-iff] |
Thm*  x,z,y,w:T List. ||x|| = ||z|| x,z,y,w:T List. ||x|| = ||z||   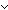 ||y|| = ||w|| ||y|| = ||w||     (x @ y) = (z @ w) (x @ y) = (z @ w)   x = z & y = w x = z & y = w | [append_one_one] |
Thm*  a,b:T List, x:T. [x] = (a @ b) a,b:T List, x:T. [x] = (a @ b)   a = nil & b = [x] a = nil & b = [x] 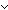 b = nil & a = [x] b = nil & a = [x] | [append_is_singleton] |
Thm*  a,c,b,d:T List. (a @ b) = (c @ d) a,c,b,d:T List. (a @ b) = (c @ d)   ( ( e:T List. a = (c @ e) & d = (e @ b) e:T List. a = (c @ e) & d = (e @ b) 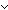 c = (a @ e) & b = (e @ d)) c = (a @ e) & b = (e @ d)) | [equal_appends] |
Thm*  P:(T P:(T   ), L2,L1:T List. list_accum(l,x.if P(x) ), L2,L1:T List. list_accum(l,x.if P(x) [x / l] else l fi;L1;L2) ~ (rev(filter(P;L2)) @ L1) [x / l] else l fi;L1;L2) ~ (rev(filter(P;L2)) @ L1) | [filter_list_accum] |
Thm*  a,b,c:Top List. ((a @ b) @ c) ~ (a @ b @ c) a,b,c:Top List. ((a @ b) @ c) ~ (a @ b @ c) | [append_assoc_sq] |
Thm*  L:T List, x,y:T. x before y L:T List, x,y:T. x before y  L L   ( ( A,B:T List. L = (A @ B) & (x A,B:T List. L = (A @ B) & (x  A) & (y A) & (y  B)) B)) | [l_before_decomp] |
Thm*  A,B:T List, x,y:T. x before y A,B:T List, x,y:T. x before y  A @ B A @ B   x before y x before y  A A 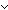 x before y x before y  B B 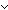 (x (x  A) & (y A) & (y  B) B) | [l_before_append_iff] |
Thm*  C,A,B:T List. C C,A,B:T List. C 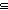 A @ B A @ B   ( ( A',B':T List. C = (A' @ B') & A' A',B':T List. C = (A' @ B') & A' 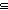 A & B' A & B' 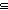 B) B) | [sublist_append_iff] |
Thm* ( x,y:T. Dec(x = y)) x,y:T. Dec(x = y))   ( ( s:T List, z:T. (z s:T List, z:T. (z  s) s)   ( ( s1,s2:T List. s = (s1 @ [z / s2]) & s1,s2:T List. s = (s1 @ [z / s2]) &  (z (z  s1))) s1))) | [l_member_decomp2] |
Thm*  s:T List, z:T. (z s:T List, z:T. (z  s) s)   ( ( s1,s2:T List. s = (s1 @ [z / s2])) s1,s2:T List. s = (s1 @ [z / s2])) | [l_member_decomp] |
Thm*  l1,l2:Top List, f,y:Top. list_accum(x,a.f(x,a);y;l1 @ l2) ~ list_accum(x,a.f(x,a);list_accum(x,a.f(x,a);y;l1);l2) l1,l2:Top List, f,y:Top. list_accum(x,a.f(x,a);y;l1 @ l2) ~ list_accum(x,a.f(x,a);list_accum(x,a.f(x,a);y;l1);l2) | [list_accum_append] |
Thm*  L:Top List, n:{0...||L||}. (firstn(n;L) @ nth_tl(n;L)) ~ L L:Top List, n:{0...||L||}. (firstn(n;L) @ nth_tl(n;L)) ~ L | [append_firstn_lastn_sq] |
Thm*  x,y,z:T List. (x @ z) = (y @ z) x,y,z:T List. (x @ z) = (y @ z)   x = y x = y | [equal_append_front] |
Thm*  l1,l2:T List. nil = (l1 @ l2) l1,l2:T List. nil = (l1 @ l2)   l1 = nil & l2 = nil l1 = nil & l2 = nil | [nil_is_append] |
Thm*  s:T List. 0 < ||s|| s:T List. 0 < ||s||   (s ~ (firstn(||s||-1;s) @ [s[(||s||-1)]])) (s ~ (firstn(||s||-1;s) @ [s[(||s||-1)]])) | [list-decomp-last] |
Thm*  i,j,k: i,j,k: . i . i j j   j j k k   (upto(i;k) ~ (upto(i;j) @ upto(j;k))) (upto(i;k) ~ (upto(i;j) @ upto(j;k))) | [append_upto] |
Thm*  P:(T P:(T   ), T':Type, f:({x:T| P(x) } ), T':Type, f:({x:T| P(x) }  T'), L1,L2:T List. mapfilter(f;P;L1 @ L2) = (mapfilter(f;P;L1) @ mapfilter(f;P;L2)) T'), L1,L2:T List. mapfilter(f;P;L1 @ L2) = (mapfilter(f;P;L1) @ mapfilter(f;P;L2)) | [mapfilter_append] |
Thm*  x1,z,x2,x3:T List. ||x1|| = ||z|| x1,z,x2,x3:T List. ||x1|| = ||z||     (x1 @ x2) = (z @ x3) (x1 @ x2) = (z @ x3)   x1 = z & x2 = x3 x1 = z & x2 = x3 | [equal_appends_eq] |
Thm*  x1,z,x2,x3:T List. ||z|| x1,z,x2,x3:T List. ||z|| ||x1|| ||x1||   (x1 @ x2) = (z @ x3) (x1 @ x2) = (z @ x3)   ( ( z':T List. x1 = (z @ z') & x3 = (z' @ x2)) z':T List. x1 = (z @ z') & x3 = (z' @ x2)) | [equal_appends_case2] |
Thm*  x1,z,x2,x3:T List. ||x1|| x1,z,x2,x3:T List. ||x1|| ||z|| ||z||   (x1 @ x2) = (z @ x3) (x1 @ x2) = (z @ x3)   ( ( z':T List. z = (x1 @ z') & x2 = (z' @ x3)) z':T List. z = (x1 @ z') & x2 = (z' @ x3)) | [equal_appends_case1] |