| 1 | 1. T: Type
2. l1: T List
3. l2: T List
4.  i,j: i,j: . i < ||l1 @ l2|| . i < ||l1 @ l2||   j < ||l1 @ l2|| j < ||l1 @ l2||    i = j i = j    (l1 @ l2)[i] = (l1 @ l2)[j] (l1 @ l2)[i] = (l1 @ l2)[j]
5. x: T
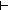  ((x ((x  l1) & (x l1) & (x  l2)) l2)) | 3 steps |
| |
| 2 | 1. T: Type
2. l1: T List
3. l2: T List
4.  i,j: i,j: . i < ||l1 @ l2|| . i < ||l1 @ l2||   j < ||l1 @ l2|| j < ||l1 @ l2||    i = j i = j    (l1 @ l2)[i] = (l1 @ l2)[j] (l1 @ l2)[i] = (l1 @ l2)[j]
5. i: 
6. j: 
7. i < ||l1||
8. j < ||l1||
9.  i = j i = j
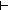  l1[i] = l1[j] l1[i] = l1[j] | 1 step |
| |
| 3 | 1. T: Type
2. l1: T List
3. l2: T List
4.  i,j: i,j: . i < ||l1 @ l2|| . i < ||l1 @ l2||   j < ||l1 @ l2|| j < ||l1 @ l2||    i = j i = j    (l1 @ l2)[i] = (l1 @ l2)[j] (l1 @ l2)[i] = (l1 @ l2)[j]
5. i: 
6. j: 
7. i < ||l2||
8. j < ||l2||
9.  i = j i = j
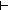  l2[i] = l2[j] l2[i] = l2[j] | 1 step |
| |
| 4 | 1. T: Type
2. l1: T List
3. l2: T List
4.  x:T. x:T.  ((x ((x  l1) & (x l1) & (x  l2)) l2))
5.  i,j: i,j: . i < ||l1|| . i < ||l1||   j < ||l1|| j < ||l1||    i = j i = j    l1[i] = l1[j] l1[i] = l1[j]
6.  i,j: i,j: . i < ||l2|| . i < ||l2||   j < ||l2|| j < ||l2||    i = j i = j    l2[i] = l2[j] l2[i] = l2[j]
7. i: 
8. j: 
9. i < ||l1 @ l2||
10. j < ||l1 @ l2||
11.  i = j i = j
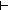  (l1 @ l2)[i] = (l1 @ l2)[j] (l1 @ l2)[i] = (l1 @ l2)[j] | 7 steps |