Thm*  a: a: , n: , n: 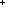 , q: , q: , r: , r: . a = q . a = q n+r n+r   r < n r < n   q = (a q = (a 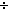 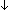 n) & r = (a mod n) n) & r = (a mod n) | [div_floor_mod_unique] |
Thm*  k1,k2: k1,k2: . .  f:(( f:(( k1+ k1+ k2) k2)   (k1+k2)). Inj( (k1+k2)). Inj( k1+ k1+ k2; k2;  (k1+k2); f) (k1+k2); f) | [union_cardinality1] |
Thm*  n: n: , f:( , f:( n n   ). increasing(f;n) ). increasing(f;n)   ( ( i: i: n, j: n, j: i. f(j) i. f(j)   (f(i))) (f(i))) | [increasing-implies2] |
Thm*  n: n: , a,b: , a,b: . sum(a+b . sum(a+b i | i < n) = ((n i | i < n) = ((n (a+a+b (a+a+b (n-1))) (n-1))) 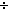 2) 2) | [sum_arith] |
Thm*  n: n: , a,b: , a,b: . sum(a+b . sum(a+b i | i < n) i | i < n) 2 = n 2 = n (a+a+b (a+a+b (n-1)) (n-1)) | [sum_arith1] |
Thm*  k: k: , f,g:( , f,g:( k k   ), p:( ), p:( k k   ). sum(if p(i) ). sum(if p(i) f(i)+g(i) else f(i) fi | i < k) = sum(f(i) | i < k)+sum(if p(i) f(i)+g(i) else f(i) fi | i < k) = sum(f(i) | i < k)+sum(if p(i) g(i) else 0 fi | i < k) g(i) else 0 fi | i < k) | [sum-ite] |
Thm*  k,b: k,b: , f:( , f:( k k   ). ( ). ( x: x: k. b k. b f(x)) f(x))   b b k k sum(f(x) | x < k) sum(f(x) | x < k) | [sum_lower_bound] |
Thm*  k,b: k,b: , f:( , f:( k k   ). ( ). ( x: x: k. f(x) k. f(x) b) b)   sum(f(x) | x < k) sum(f(x) | x < k) b b k k | [sum_bound] |
Thm*  k: k: , f,g:( , f,g:( k k   ). ( ). ( x: x: k. f(x) k. f(x) g(x)) g(x))   sum(f(x) | x < k) sum(f(x) | x < k) sum(g(x) | x < k) sum(g(x) | x < k) | [sum_le] |
Thm*  n: n: , P:( , P:( (n+1) (n+1)  Prop). ( Prop). ( x: x: (n+1). P(x)) (n+1). P(x))   P(0) & ( P(0) & ( x: x: n. P(x+1)) n. P(x+1)) | [all-nsub-add1] |
Thm*  i,j: i,j: . no_repeats( . no_repeats( ;upto(i;j)) ;upto(i;j)) | [no_repeats_upto] |
Thm*  n: n: , f,x:Top. primrec(n;x;f) ~ list_accum(i,y.f(y,i);x;upto(0;n)) , f,x:Top. primrec(n;x;f) ~ list_accum(i,y.f(y,i);x;upto(0;n)) | [primrec_list_accum] |
Thm*  R:(A R:(A  A' A'  Prop), P:(B Prop), P:(B  A A   ), P':(B ), P':(B  A' A'   ), F,G,H:(B ), F,G,H:(B  A A  A), F',G',H':(B A), F',G',H':(B  A' A'  A'), N:(B A'), N:(B  A A  (B List)), N':(B (B List)), N':(B  A' A'  (B List)), M:(A (B List)), M:(A   ), M':(A' ), M':(A'   ). ( ). ( i:B, s:A. P(i,s) i:B, s:A. P(i,s)   M(F(i,s)) M(F(i,s)) M(s)) M(s))   ( ( i:B, s:A. M(G(i,s)) i:B, s:A. M(G(i,s)) M(s)) M(s))   ( ( i:B, s:A. i:B, s:A.  P(i,s) P(i,s)   M(H(i,s)) < M(s)) M(H(i,s)) < M(s))   ( ( i:B, s:A'. P'(i,s) i:B, s:A'. P'(i,s)   M'(F'(i,s)) M'(F'(i,s)) M'(s)) M'(s))   ( ( i:B, s:A'. M'(G'(i,s)) i:B, s:A'. M'(G'(i,s)) M'(s)) M'(s))   ( ( i:B, s:A'. i:B, s:A'.  P'(i,s) P'(i,s)   M'(H'(i,s)) < M'(s)) M'(H'(i,s)) < M'(s))   ( ( j:B, u:A, v:A'. R(u,v) j:B, u:A, v:A'. R(u,v)   (P(j,u) (P(j,u)   P'(j,v))) P'(j,v)))   ( ( j:B, u:A, v:A'. R(u,v) j:B, u:A, v:A'. R(u,v)   P(j,u) P(j,u)   P'(j,v) P'(j,v)   R(F(j,u),F'(j,v))) R(F(j,u),F'(j,v)))   ( ( j:B, u:A, v:A'. R(u,v) j:B, u:A, v:A'. R(u,v)    P(j,u) P(j,u)    P'(j,v) P'(j,v)   R(H(j,u),H'(j,v))) R(H(j,u),H'(j,v)))   ( ( j:B, u:A, v:A'. R(u,v) j:B, u:A, v:A'. R(u,v)   R(G(j,u),G'(j,v))) R(G(j,u),G'(j,v)))   ( ( j:B, u:A, v:A'. R(u,v) j:B, u:A, v:A'. R(u,v)   N(j,u) = N'(j,v)) N(j,u) = N'(j,v))   ( ( j:B, u:A, v:A'. R(u,v) j:B, u:A, v:A'. R(u,v)   R(process u j where process s i == if P(i,s) then F(i,s) else G(i,s) where xs := N(i,s); s:= H(i,s); while not null xs { s := process s (hd xs); xs := tl xs; } ,process v j where process s i == if P'(i,s) then F'(i,s) else G'(i,s) where xs := N'(i,s); s:= H'(i,s); while not null xs { s := process s (hd xs); xs := tl xs; } )) R(process u j where process s i == if P(i,s) then F(i,s) else G(i,s) where xs := N(i,s); s:= H(i,s); while not null xs { s := process s (hd xs); xs := tl xs; } ,process v j where process s i == if P'(i,s) then F'(i,s) else G'(i,s) where xs := N'(i,s); s:= H'(i,s); while not null xs { s := process s (hd xs); xs := tl xs; } )) | [accumulate-rel] |
Thm*  M:(A M:(A   ), Q:(B ), Q:(B  A A  A A  Prop), P:(B Prop), P:(B  A A   ), F,G,H:(B ), F,G,H:(B  A A  A), N:(B A), N:(B  A A  (B List)). ( (B List)). ( i:B, s:A. P(i,s) i:B, s:A. P(i,s)   M(F(i,s)) M(F(i,s)) M(s)) M(s))   ( ( i:B, s:A. M(G(i,s)) i:B, s:A. M(G(i,s)) M(s)) M(s))   ( ( i:B, s:A. i:B, s:A.  P(i,s) P(i,s)   M(H(i,s)) < M(s)) M(H(i,s)) < M(s))   ( ( j:B, u:A. P(j,u) j:B, u:A. P(j,u)   Q(j,u,F(j,u))) Q(j,u,F(j,u)))   ( ( j:B, u,z:A. j:B, u,z:A.  P(j,u) P(j,u)   Q(j,H(j,u),z) Q(j,H(j,u),z)   Q(j,u,G(j,z))) Q(j,u,G(j,z)))   ( ( j:B, u:A. Q(j,u,u)) j:B, u:A. Q(j,u,u))   ( ( i,j:B, u,v,z:A. Q(i,u,v) i,j:B, u,v,z:A. Q(i,u,v)   Q(j,v,z) Q(j,v,z)   Q(j,u,z)) Q(j,u,z))   ( ( j:B, u:A. Q(j,u,process u j where process s i == if P(i,s) then F(i,s) else G(i,s) where xs := N(i,s); s:= H(i,s); while not null xs { s := process s (hd xs); xs := tl xs; } )) j:B, u:A. Q(j,u,process u j where process s i == if P(i,s) then F(i,s) else G(i,s) where xs := N(i,s); s:= H(i,s); while not null xs { s := process s (hd xs); xs := tl xs; } )) | [accumulate-induction1] |
Thm*  A,B:Type, P:(B A,B:Type, P:(B  A A   ), F,G,H:(B ), F,G,H:(B  A A  A), N:(B A), N:(B  A A  (B List)), M:(A (B List)), M:(A   ). ( ). ( i:B, s:A. P(i,s) i:B, s:A. P(i,s)   M(F(i,s)) M(F(i,s)) M(s)) M(s))   ( ( i:B, s:A. M(G(i,s)) i:B, s:A. M(G(i,s)) M(s)) M(s))   ( ( i:B, s:A. i:B, s:A.  P(i,s) P(i,s)   M(H(i,s)) < M(s)) M(H(i,s)) < M(s))   ( ( j:B, u:A. process u j where process s i == if P(i,s) then F(i,s) else G(i,s) where xs := N(i,s); s:= H(i,s); while not null xs { s := process s (hd xs); xs := tl xs; } j:B, u:A. process u j where process s i == if P(i,s) then F(i,s) else G(i,s) where xs := N(i,s); s:= H(i,s); while not null xs { s := process s (hd xs); xs := tl xs; }  {s:A| M(s) {s:A| M(s) M(u) }) M(u) }) | [accumulate_wf] |
Thm*  i,j: i,j: , k: , k: (j-i). upto(i;j)[k] = i+k (j-i). upto(i;j)[k] = i+k | [select_upto] |
Thm*  j: j: , i: , i: j. ||upto(i;j)|| = j-i j. ||upto(i;j)|| = j-i   | [length_upto] |
Thm*  i,j,k: i,j,k: . (k . (k  upto(i;j)) upto(i;j))   i i k & k < j k & k < j | [member_upto] |
Thm*  i,j: i,j: . upto(i;j) . upto(i;j)  {i..j {i..j } List } List | [upto_wf] |