| | Some definitions of interest. |
|
| append | Def as @ bs == Case of as; nil  bs ; a.as' bs ; a.as'  [a / (as' @ bs)] (recursive) [a / (as' @ bs)] (recursive) |
| | | Thm*  T:Type, as,bs:T List. (as @ bs) T:Type, as,bs:T List. (as @ bs)  T List T List |
|
| assert | Def 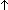 b == if b b == if b True else False fi True else False fi |
| | | Thm*  b: b: . b . b  Prop Prop |
|
| iff | Def P   Q == (P Q == (P   Q) & (P Q) & (P   Q) Q) |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A   B) B)  Prop Prop |
|
| l_before | Def x before y  l == [x; y] l == [x; y] 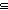 l l |
| | | Thm*  T:Type, l:T List, x,y:T. x before y T:Type, l:T List, x,y:T. x before y  l l  Prop Prop |
|
| mapfilter | Def mapfilter(f;P;L) == map(f;filter(P;L)) |
| | | Thm*  T:Type, P:(T T:Type, P:(T   ), T':Type, f:({x:T| P(x) } ), T':Type, f:({x:T| P(x) }  T'), L:T List. mapfilter(f;P;L) T'), L:T List. mapfilter(f;P;L)  T' List T' List |