| | Some definitions of interest. |
|
| gr_v | Def Vertices(t) == 1of(t) |
| | | Thm*  t:Graph. Vertices(t) t:Graph. Vertices(t)  Type Type |
|
| graph | Def Graph == v:Type e:Type e:Type (e (e  v v v) v) Top Top |
| | | Thm* Graph  Type{i'} Type{i'} |
|
| paren | Def paren(T;s) == s = nil  (T+T) List (T+T) List 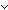 ( ( t:T, s':(T+T) List. s = ([inl(t)] @ s' @ [inr(t)]) & paren(T;s')) t:T, s':(T+T) List. s = ([inl(t)] @ s' @ [inr(t)]) & paren(T;s')) 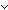 ( ( s',s'':(T+T) List. ||s'|| < ||s|| & ||s''|| < ||s|| & s = (s' @ s'') & paren(T;s') & paren(T;s'')) (recursive) s',s'':(T+T) List. ||s'|| < ||s|| & ||s''|| < ||s|| & s = (s' @ s'') & paren(T;s') & paren(T;s'')) (recursive) |
| | | Thm*  T:Type, s:(T+T) List. paren(T;s) T:Type, s:(T+T) List. paren(T;s)  Prop Prop |