| 2 | 9.  L:Vertices(the_graph) List, s:traversal(the_graph). L:Vertices(the_graph) List, s:traversal(the_graph).
 s2:traversal(the_graph). list_accum(s',j.dfs(the_obj;s';j);s;L) = (s2 @ s) s2:traversal(the_graph). list_accum(s',j.dfs(the_obj;s';j);s;L) = (s2 @ s)
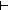  s':traversal(the_graph). ((inr(i) s':traversal(the_graph). ((inr(i)  s) s) 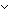 (inl(i) (inl(i)  s) s)   s' = nil) & ( s' = nil) & ( (inr(i) (inr(i)  s) & s) &  (inl(i) (inl(i)  s) s)   ( ( s2:traversal(the_graph). s' = ([inl(i)] @ s2 @ [inr(i)]) s2:traversal(the_graph). s' = ([inl(i)] @ s2 @ [inr(i)])  traversal(the_graph))) & [inl(i) / (the_obj.eacc(( traversal(the_graph))) & [inl(i) / (the_obj.eacc(( s',j. dfs(the_obj;s';j)),[inr(i) / s],i))] = (s' @ s) s',j. dfs(the_obj;s';j)),[inr(i) / s],i))] = (s' @ s)  traversal(the_graph) traversal(the_graph) | 4 steps |