| 1 | 4.  s1,s2:traversal(the_graph), i:Vertices(the_graph).
P(i,s1,s2) s1,s2:traversal(the_graph), i:Vertices(the_graph).
P(i,s1,s2)   l_disjoint(Vertices(the_graph)+Vertices(the_graph);s2;s1) l_disjoint(Vertices(the_graph)+Vertices(the_graph);s2;s1)
5.  s1,s2:traversal(the_graph), i:Vertices(the_graph).
P(i,s1,s2) s1,s2:traversal(the_graph), i:Vertices(the_graph).
P(i,s1,s2)   no_repeats(Vertices(the_graph)+Vertices(the_graph);s2) no_repeats(Vertices(the_graph)+Vertices(the_graph);s2)
6.  s:traversal(the_graph), i:Vertices(the_graph). member-paren(x,y.the_obj.eq(x,y);i;s) s:traversal(the_graph), i:Vertices(the_graph). member-paren(x,y.the_obj.eq(x,y);i;s)   P(i,s,nil) P(i,s,nil)
7.  s1,s2,s3:traversal(the_graph), i,j:Vertices(the_graph).
i-the_graph- > j s1,s2,s3:traversal(the_graph), i,j:Vertices(the_graph).
i-the_graph- > j   P(j,s1,s2) P(j,s1,s2)   P(i,s2 @ s1,s3) P(i,s2 @ s1,s3)   P(i,s1,s3 @ s2) P(i,s1,s3 @ s2)
8.  s1,s2:traversal(the_graph), i:Vertices(the_graph). s1,s2:traversal(the_graph), i:Vertices(the_graph).
 member-paren(x,y.the_obj.eq(x,y);i;s1) member-paren(x,y.the_obj.eq(x,y);i;s1)
  P(i,[inr(i) / s1],s2)
P(i,[inr(i) / s1],s2)   P(i,s1,[inl(i) / (s2 @ [inr(i)])]) P(i,s1,[inl(i) / (s2 @ [inr(i)])])
9. M: traversal(the_graph)  
10.  i:Vertices(the_graph), s:traversal(the_graph). M([inl(i) / s]) i:Vertices(the_graph), s:traversal(the_graph). M([inl(i) / s])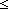 M(s) M(s)
11.  i:Vertices(the_graph), s:traversal(the_graph). i:Vertices(the_graph), s:traversal(the_graph).
 member-paren(x,y.the_obj.eq(x,y);i;s) member-paren(x,y.the_obj.eq(x,y);i;s)   M([inr(i) / s]) < M(s) M([inr(i) / s]) < M(s)
12.  x,y:Vertices(the_graph). the_obj.eq(x,y) x,y:Vertices(the_graph). the_obj.eq(x,y)   x = y x = y
13.  T:Type, s:T, x:Vertices(the_graph), f:(T T:Type, s:T, x:Vertices(the_graph), f:(T  Vertices(the_graph) Vertices(the_graph)  T). T).
 L:Vertices(the_graph) List.
( L:Vertices(the_graph) List.
( y:Vertices(the_graph). x-the_graph- > y y:Vertices(the_graph). x-the_graph- > y   (y (y  L))
& the_obj.eacc(f,s,x) = list_accum(s',x'.f(s',x');s;L) L))
& the_obj.eacc(f,s,x) = list_accum(s',x'.f(s',x');s;L)
14.  T:Type, s:T, f:(T T:Type, s:T, f:(T  Vertices(the_graph) Vertices(the_graph)  T). T).
 L:Vertices(the_graph) List.
no_repeats(Vertices(the_graph);L)
& ( L:Vertices(the_graph) List.
no_repeats(Vertices(the_graph);L)
& ( y:Vertices(the_graph). (y y:Vertices(the_graph). (y  L))
& the_obj.vacc(f,s) = list_accum(s',x'.f(s',x');s;L) L))
& the_obj.vacc(f,s) = list_accum(s',x'.f(s',x');s;L)
15. d: 
16.  d1: d1: .
d1 < d .
d1 < d
  (
( s:traversal(the_graph), i:Vertices(the_graph).
M(s) s:traversal(the_graph), i:Vertices(the_graph).
M(s)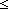 d1 d1   ( ( s':traversal(the_graph). M(s' @ s) s':traversal(the_graph). M(s' @ s)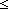 M(s) & P(i,s,s') & dfs(the_obj;s;i) = (s' @ s))) M(s) & P(i,s,s') & dfs(the_obj;s;i) = (s' @ s)))
17. s: traversal(the_graph)
18. i: Vertices(the_graph)
19. M(s)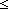 d d
20.  member-paren(x,y.the_obj.eq(x,y);i;s) member-paren(x,y.the_obj.eq(x,y);i;s)
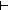  s':traversal(the_graph). M(s' @ s) s':traversal(the_graph). M(s' @ s)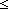 M(s) & P(i,s,s') & [inl(i) / (the_obj.eacc(( M(s) & P(i,s,s') & [inl(i) / (the_obj.eacc(( s',j. dfs(the_obj;s';j)),[inr(i) / s],i))] = (s' @ s) s',j. dfs(the_obj;s';j)),[inr(i) / s],i))] = (s' @ s)  traversal(the_graph) traversal(the_graph) | 19 steps |