| By: |
RewriteOfThm
Thm* all
Thm* (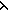 k:hnum. all k:hnum. all
Thm* ( k:hnum. ( k:hnum. (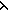 n:hnum. implies n:hnum. implies
Thm* ( k:hnum. ( k:hnum. ( n:hnum. (lt(0,n) n:hnum. (lt(0,n)
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,exists n:hnum. ,exists
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,( n:hnum. ,(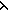 r:hnum. exists r:hnum. exists
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,( n:hnum. ,( r:hnum. ( r:hnum. (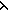 q:hnum. and q:hnum. and
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,( n:hnum. ,( r:hnum. ( r:hnum. ( q:hnum. (equal(k,add(mult(q,n),r)) q:hnum. (equal(k,add(mult(q,n),r))
Thm* ( k:hnum. ( k:hnum. ( n:hnum. ,( n:hnum. ,( r:hnum. ( r:hnum. ( q:hnum. ,lt(r,n))))))) q:hnum. ,lt(r,n)))))))
(SimpsetC [`hol_to_nuprl`;`bequal`]) |