Thm*  'a:S. ( 'a:S. ( 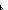 x:'a. false x:'a. false ) = false ) = false | [ball_bfalse] |
Thm*  'a:S. ( 'a:S. ( 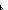 x:'a. true x:'a. true ) = true ) = true | [ball_btrue] |
Thm*  'a:S. ( 'a:S. (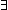 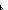 x:'a. false x:'a. false ) = false ) = false | [bexists_bfalse] |
Thm*  'a:S. ( 'a:S. (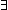 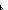 x:'a. true x:'a. true ) = true ) = true | [bexists_btrue] |
Thm*  p: p: . false . false = p = p 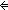 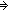 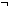 p p | [equal_bfalse_to_assert_2] |
Thm*  p: p: . p = false . p = false 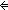 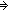 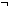 p p | [equal_bfalse_to_assert] |
Thm*  p: p: . true . true = p = p 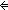 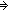 p p | [equal_btrue_to_assert_2] |
Thm*  p: p: . p = true . p = true 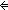 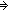 p p | [equal_btrue_to_assert] |
Thm*  'a:S, x:'a. (x = 'a:S, x:'a. (x =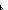 x) = true x) = true | [bequal_refl_simp] |
Thm* 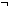  false false = true = true | [bnot_simp_2] |
Thm* 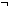  true true = false = false | [bnot_simp_1] |
Thm*  b: b: . (b . (b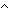  false false ) = false ) = false | [band_simp_2] |
Thm*  b: b: . (true . (true 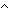  b) = b b) = b | [band_simp_3] |
Thm*  b: b: . (false . (false 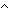  b) = false b) = false | [band_simp_4] |
Thm*  b: b: . (false . (false 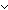  b) = b b) = b | [bor_simp_4] |
Thm*  b: b: . (true . (true 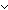  b) = true b) = true | [bor_simp_3] |
Thm*  b: b: . (b . (b 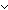  false false ) = b ) = b | [bor_simp_2] |
Thm*  b: b: . (b . (b 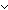  true true ) = true ) = true | [bor_simp_1] |
Thm*  b: b: . (b . (b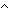  true true ) = b ) = b | [band_simp_1] |
Thm*  p:('a p:('a   ). ).
Thm* b_exists_unique('a;x.p(x))
Thm* 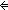 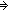
Thm* (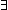 x:'a. p(x)) & ( x:'a. p(x)) & ( x,y:'a. p(x) & p(y) x,y:'a. p(x) & p(y) 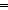 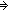 x = y) x = y) | [assert_of_b_exists_unique] |
Def type_definition ==  P:'a P:'a   . .  rep:'b rep:'b  'a. 'a.  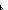 type_definition('a;'b;P;rep) type_definition('a;'b;P;rep) | [htype_definition] |
Def cond ==  b: b: . .  p:'a. p:'a.  q:'a. if b then p else q fi q:'a. if b then p else q fi | [hcond] |
Def exists_unique ==  p:'a p:'a   . b_exists_unique('a;x.p(x)) . b_exists_unique('a;x.p(x)) | [hexists_unique] |
Def not ==  p: p: . . 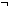  p p | [hnot] |
Def or ==  p: p: . .  q: q: . p . p 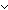  q q | [hor] |
Def and ==  p: p: . .  q: q: . p . p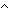  q q | [hand] |
Def all ==  p:'a p:'a   . .  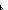 x:'a. (p(x)) x:'a. (p(x)) | [hall] |
Def exists ==  p:'a p:'a   . . 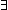 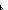 x:'a. (p(x)) x:'a. (p(x)) | [hexists] |