Thm*  'a:S. iso_pair('a List;( 'a:S. iso_pair('a List;(  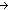 'a) 'a)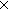  ;is_list_rep;rep_list;abs_list) ;is_list_rep;rep_list;abs_list) | [list_iso] |
Thm*  'a:S, n: 'a:S, n: , l:'a List. n<||l|| , l:'a List. n<||l|| 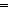 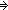 el(n,l) = l[n] el(n,l) = l[n] | [hel_nuprl] |
Thm* it_sum(nil) = 0
Thm* & ( l: l: List. List. 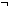 mt(l) mt(l) 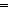 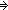 it_sum(l) = head(l)+it_sum(tl(l))) it_sum(l) = head(l)+it_sum(tl(l)))
Thm* & ( x: x: , l: , l: List. it_sum(cons(x; l)) = x+it_sum(l)) List. it_sum(cons(x; l)) = x+it_sum(l)) | [it_sum_def] |
Thm*  l: l: List. it_sum(l) List. it_sum(l) 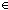  | [it_sum_wf] |
Thm*  'a:S, l:'a List. rep_list('a;l) 'a:S, l:'a List. rep_list('a;l) 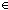 ( (  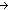 'a) 'a)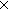  | [rep_list_wf] |
Thm*  'a:Type, l:'a List. ||l|| 'a:Type, l:'a List. ||l|| 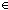  | [length_wf_nat] |
Def el == 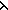 n: n: . . 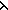 l:'a List. if n= l:'a List. if n=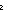 0 then hd(l) else el(n-1,tl(l)) fi 0 then hd(l) else el(n-1,tl(l)) fi
Def (recursive) | [hel] |
Def it_sum == 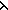 l: l: List. it_sum(l) List. it_sum(l) | [hit_sum] |
Def abs_list == 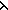 r:( r:(  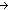 'a) 'a)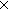  . @a:'a List. (r = rep_list('a;a)) . @a:'a List. (r = rep_list('a;a)) | [habs_list] |
Def is_list_rep
Def == 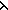 r:( r:(  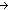 'a) 'a)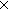  . . 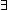  f: f:  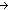 'a 'a
Def ==  r:( r:(   'a) 'a)  . .   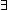 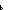 n: n:
Def ==  r:( r:(   'a) 'a)  . .     (r (r
Def ==  r:( r:(   'a) 'a)  . .     = =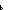 < <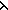 m: m: . if m< . if m<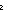 n then f(m) else @ n then f(m) else @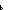 x:'a. true x:'a. true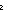 fi ,n>) fi ,n>) | [his_list_rep] |
Def rep_list('a;l) == <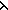 n: n: . if n< . if n<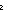 ||l|| then l[n] else arb('a) fi ,||l||> ||l|| then l[n] else arb('a) fi ,||l||> | [rep_list] |