| | Some definitions of interest. |
|
| habs_num | Def abs_num ==  n: n: . @m: . @m: . (n = rep_num(m) . (n = rep_num(m)   ) ) |
| | | Thm* abs_num  (hind (hind   hnum) hnum) |
|
| hrep_num | Def rep_num ==  n: n: . ncompose(suc_rep;n;zero_rep) . ncompose(suc_rep;n;zero_rep) |
| | | Thm* rep_num  (hnum (hnum   hind) hind) |
|
| choose | Def @x:T. P(x) == InjCase(lem({x:T| P(x) }); x. x, arb(T)) |
| | | Thm*  T:S, P:(T T:S, P:(T  Type). (@x:T. P(x)) Type). (@x:T. P(x))  T T |
|
| hnum | Def hnum ==  |
| | | Thm* hnum  S S |
|
| nat | Def  == {i: == {i: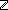 | 0 | 0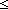 i } i } |
| | | Thm*   Type Type |
| | | Thm*   S S |