| | Some definitions of interest. |
|
| hall | Def all ==  p:'a p:'a  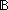 . .  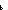 x:'a. (p(x)) x:'a. (p(x)) |
| | | Thm*  'a:S. all 'a:S. all  (('a (('a   hbool) hbool)   hbool) hbool) |
|
| ball | Def  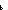 x:T. P(x) == x:T. P(x) == 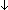 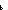 ( ( x:T. x:T. 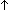 P(x)) P(x)) |
| | | Thm*  T:Type, P:(T T:Type, P:(T  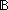 ). ( ). ( 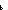 x:T. P(x)) x:T. P(x))  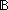 |
|
| hselect | Def select ==  p:'a p:'a  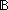 . @ . @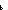 x:'a. (p(x)) x:'a. (p(x)) |
| | | Thm*  'a:S. select 'a:S. select  (('a (('a   hbool) hbool)   'a) 'a) |
|
| bchoose | Def @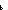 x:'a. p(x) == @x:'a. x:'a. p(x) == @x:'a. 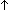 p(x) p(x) |
| | | Thm*  'a:S, p:('a 'a:S, p:('a  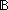 ). (@ ). (@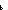 x:'a. p(x)) x:'a. p(x))  'a 'a |
|
| assert | Def 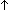 b == if b b == if b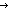 True else False fi True else False fi |
| | | Thm*  b: b: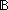 . b . b  Prop Prop |
|
| hequal | Def equal ==  x:'a. x:'a.  y:'a. x = y:'a. x =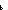 y y |
| | | Thm*  'a:S. equal 'a:S. equal  ('a ('a   'a 'a   hbool) hbool) |
|
| bequal | Def x =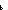 y == y == 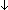 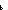 (x = y (x = y  T) T) |
| | | Thm*  T:Type, x,y:T. (x = T:Type, x,y:T. (x =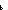 y) y)  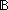 |
|
| hnot | Def not ==  p: p: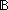 . . 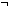 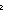 p p |
| | | Thm* not  (hbool (hbool   hbool) hbool) |
|
| bnot | Def 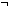 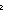 b == if b b == if b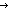 false false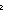 else true else true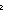 fi fi |
| | | Thm*  b: b: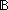 . . 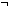 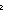 b b  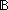 |
|
| hzero_rep | Def zero_rep == @x: . ( . ( y: y: . . 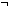 x = suc_rep(y) x = suc_rep(y)   ) ) |
| | | Thm* zero_rep  hind hind |
|
| hsuc_rep | Def suc_rep ==  x: x: . (@f: . (@f:    . (one_one( . (one_one( ; ; ;f) & ;f) & 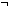 onto( onto( ; ; ;f)))(x) ;f)))(x) |
| | | Thm* suc_rep  (hind (hind   hind) hind) |
|
| choose | Def @x:T. P(x) == InjCase(lem({x:T| P(x) }); x. x, arb(T)) |
| | | Thm*  T:S, P:(T T:S, P:(T  Type). (@x:T. P(x)) Type). (@x:T. P(x))  T T |
|
| hind | Def hind ==  |
| | | Thm* hind  S S |
|
| nat | Def  == {i: == {i: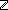 | 0 | 0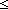 i } i } |
| | | Thm*   Type Type |
| | | Thm*   S S |
|
| not | Def 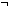 A == A A == A 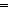 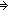 False False |
| | | Thm*  A:Prop. ( A:Prop. (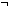 A) A)  Prop Prop |
|
| tlambda | Def ( x:T. b(x))(x) == b(x) x:T. b(x))(x) == b(x) |