| | Some definitions of interest. |
|
| hsimp_rec_fun | Def simp_rec_fun
Def ==  x:'a. x:'a.  f:'a f:'a  'a. 'a.  n: n: . @ . @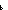 fun: fun:   'a. (simp_rec_rel(fun,x,f,n)) 'a. (simp_rec_rel(fun,x,f,n)) |
| | | Thm*  'a:S. simp_rec_fun 'a:S. simp_rec_fun  ('a ('a   ('a ('a   'a) 'a)   hnum hnum   hnum hnum   'a) 'a) |
|
| bchoose | Def @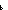 x:'a. p(x) == @x:'a. x:'a. p(x) == @x:'a. 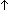 p(x) p(x) |
| | | Thm*  'a:S, p:('a 'a:S, p:('a  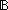 ). (@ ). (@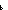 x:'a. p(x)) x:'a. p(x))  'a 'a |
|
| hfun | Def 'a   'b == 'a 'b == 'a  'b 'b |
| | | Thm*  'a,'b:S. ('a 'a,'b:S. ('a   'b) 'b)  S S |
|
| hsimp_rec_rel | Def simp_rec_rel
Def ==  fun: fun:   'a. 'a.  x:'a. x:'a.  f:'a f:'a  'a. 'a.  n: n: . . 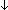 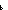 (fun(0) = x (fun(0) = x
Def == & ( m: m: . m<n . m<n 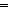 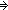 fun(m+1) = f(fun(m)))) fun(m+1) = f(fun(m)))) |
| | | Thm*  'a:S. simp_rec_rel 'a:S. simp_rec_rel  ((hnum ((hnum   'a) 'a)   'a 'a   ('a ('a   'a) 'a)   hnum hnum   hbool) hbool) |
|
| nat | Def  == {i: == {i: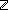 | 0 | 0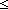 i } i } |
| | | Thm*   Type Type |
| | | Thm*   S S |
|
| ncompose | Def ncompose(f;n;x) == if n=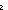 0 then x else f(ncompose(f;n-1;x)) fi (recursive) 0 then x else f(ncompose(f;n-1;x)) fi (recursive) |
| | | Thm*  'a:Type, n: 'a:Type, n: , x:'a, f:('a , x:'a, f:('a  'a). ncompose(f;n;x) 'a). ncompose(f;n;x)  'a 'a |
|
| stype | Def S == {T:Type| 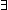 x:T. True } x:T. True } |
| | | Thm* S  Type{2} Type{2} |