| | Some definitions of interest. |
|
| hall | Def all ==  p:'a p:'a   . .  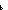 x:'a. (p(x)) x:'a. (p(x)) |
| | | Thm*  'a:S. all 'a:S. all  (('a (('a   hbool) hbool)   hbool) hbool) |
|
| assert | Def 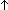 b == if b b == if b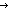 True else False fi True else False fi |
| | | Thm*  b: b: . b . b  Prop Prop |
|
| hand | Def and ==  p: p: . .  q: q: . p . p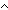 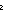 q q |
| | | Thm* and  (hbool (hbool   hbool hbool   hbool) hbool) |
|
| hinl | Def inl ==  x:'a. inl(x) x:'a. inl(x) |
| | | Thm*  'a,'b:S. inl 'a,'b:S. inl  ('a ('a   hsum('a; 'b)) hsum('a; 'b)) |
|
| hinr | Def inr ==  x:'b. inr(x) x:'b. inr(x) |
| | | Thm*  'b,'a:S. inr 'b,'a:S. inr  ('b ('b   hsum('a; 'b)) hsum('a; 'b)) |
|
| hisl | Def isl ==  u:'a+'b. isl(u) u:'a+'b. isl(u) |
| | | Thm*  'a,'b:S. isl 'a,'b:S. isl  (hsum('a; 'b) (hsum('a; 'b)   hbool) hbool) |
|
| hnot | Def not ==  p: p: . . 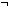 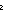 p p |
| | | Thm* not  (hbool (hbool   hbool) hbool) |
|
| label | Def t ...$L == t |
|
| stype | Def S == {T:Type| 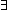 x:T. True } x:T. True } |
| | | Thm* S  Type{2} Type{2} |
|
| tlambda | Def ( x:T. b(x))(x) == b(x) x:T. b(x))(x) == b(x) |