| | Some definitions of interest. |
|
| action | Def action(dec) == Unit+(k:Knd dec(k)) dec(k)) |
| | | Thm*  dec:(Knd dec:(Knd  Type). action(dec) Type). action(dec)  Type Type |
|
| Knd | Def Knd == (IdLnk Id)+Id Id)+Id |
| | | Thm* Knd  Type Type |
|
| Msg | Def Msg(M) == l:IdLnk t:Id t:Id M(l,t) M(l,t) |
| | | Thm*  M:(IdLnk M:(IdLnk  Id Id  Type). Msg(M) Type). Msg(M)  Type Type |
|
| IdLnk | Def IdLnk == Id Id Id  |
| | | Thm* IdLnk  Type Type |
|
| Id | Def Id == Atom  |
| | | Thm* Id  Type Type |
|
| w-action-dec | Def w-action-dec(TA;M;i)(k)
Def == kindcase(k;a.TA(i,a);l,tg.if destination(l) = i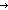 M(l,tg) else Void fi) M(l,tg) else Void fi) |
|
| assert | Def  b == if b b == if b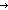 True else False fi True else False fi |
| | | Thm*  b: b: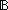 . b . b  Prop Prop |
|
| isl | Def isl(x) == InjCase(x; y. true ; z. false ; z. false ) ) |
| | | Thm*  A,B:Type, x:A+B. isl(x) A,B:Type, x:A+B. isl(x)  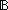 |
|
| lsrc | Def source(l) == 1of(l) |
| | | Thm*  l:IdLnk. source(l) l:IdLnk. source(l)  Id Id |
|
| mlnk | Def mlnk(m) == 1of(m) |
| | | Thm*  M:(IdLnk M:(IdLnk  Id Id  Type), m:Msg(M). mlnk(m) Type), m:Msg(M). mlnk(m)  IdLnk IdLnk |
| | | Thm*  the_es:ES, m:Msg. mlnk(m) the_es:ES, m:Msg. mlnk(m)  IdLnk IdLnk |
|
| nat | Def  == {i: == {i: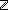 | 0 | 0 i } i } |
| | | Thm*   Type Type |
|
| not | Def  A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. ( A) A)  Prop Prop |
|
| outr | Def outr(x) == InjCase(x; y. "???"; z. z) |
| | | Thm*  A,B:Type, x:A+B. A,B:Type, x:A+B.   isl(x) isl(x)   outr(x) outr(x)  B B |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| top | Def Top == Void given Void |
| | | Thm* Top  Type Type |