| | Some definitions of interest. |
|
| deq | Def EqDecider(T) == eq:T  T T  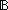   x,y:T. x = y x,y:T. x = y 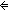   (eq(x,y)) (eq(x,y)) |
| | | Thm*  T:Type. EqDecider(T) T:Type. EqDecider(T)  Type Type |
|
| assert | Def  b == if b b == if b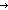 True else False fi True else False fi |
| | | Thm*  b: b: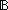 . b . b  Prop Prop |
|
| fpf | Def a:A fp-> B(a) == d:A List a:{a:A| (a a:{a:A| (a  d) } d) }  B(a) B(a) |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type). a:A fp-> B(a) Type). a:A fp-> B(a)  Type Type |
|
| fpf-dom | Def x  dom(f) == deq-member(eq;x;1of(f)) dom(f) == deq-member(eq;x;1of(f)) |
|
| so_lambda1 | Def (  1. b(1))(1) == b(1) 1. b(1))(1) == b(1) |
|
| top | Def Top == Void given Void |
| | | Thm* Top  Type Type |