| | Some definitions of interest. |
|
| dsys | Def Dsys == Id  MsgA MsgA |
| | | Thm* Dsys  Type{i'} Type{i'} |
|
| interface-check | Def interface-check(D;l;tg;T) == T  r M(destination(l)).din(l,tg) r M(destination(l)).din(l,tg) |
|
| ma-feasible | Def Feasible(M)
Def ==  x x dom(1of(M)). T=1of(M)(x) dom(1of(M)). T=1of(M)(x)   T T
Def == &  k k dom(1of(2of(M))). T=1of(2of(M))(k) dom(1of(2of(M))). T=1of(2of(M))(k)   Dec(T) Dec(T)
Def == &  a a dom(1of(2of(2of(2of(M))))). p=1of(2of(2of(2of(M))))(a) dom(1of(2of(2of(2of(M))))). p=1of(2of(2of(2of(M))))(a)  
Def == & s:State(1of(M)). Dec( s:State(1of(M)). Dec( v:1of(2of(M))(locl(a))?Top. p(s,v)) v:1of(2of(M))(locl(a))?Top. p(s,v))
Def == &  kx kx dom(1of(2of(2of(2of(2of(M)))))). dom(1of(2of(2of(2of(2of(M)))))).
Def == ef=1of(2of(2of(2of(2of(M)))))(kx)   M.frame(1of(kx) affects 2of(kx)) M.frame(1of(kx) affects 2of(kx))
Def == &  kl kl dom(1of(2of(2of(2of(2of(2of(M))))))). dom(1of(2of(2of(2of(2of(2of(M))))))).
Def == & snd=1of(2of(2of(2of(2of(2of(M))))))(kl)    tg:Id. tg:Id.
Def == & (tg  map( map( p.1of(p);snd)) p.1of(p);snd))   M.sframe(1of(kl) sends <2of(kl),tg>) M.sframe(1of(kl) sends <2of(kl),tg>) |
|
| ma-outlinks | Def ma-outlinks(M;i) == da-outlinks(1of(2of(M));i) |
|
| IdLnk | Def IdLnk == Id Id Id  |
| | | Thm* IdLnk  Type Type |
|
| ma-sends-on | Def M sends on link l
Def == deq-member(IdLnkDeq;l;map( p. p.
Def == 2of(p);1of(1of(2of(2of(2of(2of(2of(M))))))))) |
|
| Id | Def Id == Atom  |
| | | Thm* Id  Type Type |
|
| assert | Def  b == if b b == if b True else False fi True else False fi |
| | | Thm*  b: b: . b . b  Prop Prop |
|
| d-m | Def M(i) == D(i) |
|
| l_all | Def ( x x L.P(x)) == L.P(x)) ==  x:T. (x x:T. (x  L) L)   P(x) P(x) |
| | | Thm*  T:Type, L:T List, P:(T T:Type, L:T List, P:(T  Prop). ( Prop). ( x x L.P(x)) L.P(x))  Prop Prop |
|
| l_member | Def (x  l) == l) ==  i: i: . i<||l|| & x = l[i] . i<||l|| & x = l[i]  T T |
| | | Thm*  T:Type, x:T, l:T List. (x T:Type, x:T, l:T List. (x  l) l)  Prop Prop |
|
| ldst | Def destination(l) == 1of(2of(l)) |
| | | Thm*  l:IdLnk. destination(l) l:IdLnk. destination(l)  Id Id |
|
| lsrc | Def source(l) == 1of(l) |
| | | Thm*  l:IdLnk. source(l) l:IdLnk. source(l)  Id Id |
|
| ma-is-empty | Def ma-is-empty(M)
Def == fpf-is-empty(1of(M))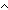  fpf-is-empty(1of(2of(M))) fpf-is-empty(1of(2of(M)))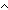 
Def == fpf-is-empty(1of(2of(2of(M))))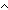  fpf-is-empty(1of(2of(2of(2of(M))))) fpf-is-empty(1of(2of(2of(2of(M)))))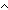 
Def == fpf-is-empty(1of(2of(2of(2of(2of(M))))))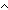 
Def == fpf-is-empty(1of(2of(2of(2of(2of(2of(M)))))))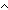 
Def == fpf-is-empty(1of(2of(2of(2of(2of(2of(2of(M))))))))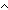 
Def == fpf-is-empty(1of(2of(2of(2of(2of(2of(2of(2of(M))))))))) |
|
| map | Def map(f;as) == Case of as; nil  nil ; a.as' nil ; a.as'  [(f(a)) / map(f;as')] [(f(a)) / map(f;as')]
Def (recursive) |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B), l:A List. map(f;l) B), l:A List. map(f;l)  B List B List |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B), l:A List B), l:A List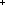 . map(f;l) . map(f;l)  B List B List |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 2of(p) B(a)). 2of(p)  B(1of(p)) B(1of(p)) |