| | Some definitions of interest. |
|
| bi-tree | Def bi-tree(T;to;from)
Def == bi-graph(T;to;from)
Def == & ( i,j:|T|. i,j:|T|.
Def == & (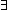 p:Edge(T) List. p:Edge(T) List.
Def == & (lconnects(p;i;j) & ( q:Edge(T) List. lconnects(q;i;j) q:Edge(T) List. lconnects(q;i;j) 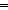  q = p)) q = p))
Def == & (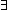 L:|T| List. L:|T| List.  i:|T|. (i i:|T|. (i  L)) L))
Def == & |T| |
|
| bi-graph | Def bi-graph(G;to;from)
Def ==  i:|G|. i:|G|.
Def == ( l l to(i).destination(l) = i to(i).destination(l) = i
Def == & 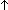 (G(source(l))) (G(source(l)))
Def == & (l  from(source(l))) from(source(l)))
Def == & (lnk-inv(l)  from(i))) from(i)))
Def == & ( l l from(i).source(l) = i from(i).source(l) = i
Def == & & 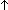 (G(destination(l))) (G(destination(l)))
Def == & & (l  to(destination(l))) to(destination(l)))
Def == & & (lnk-inv(l)  to(i))) to(i))) |
|
| spanner | Def spanner(f;T;to;from)
Def == ( l:Edge(T). f(l) = l:Edge(T). f(l) = 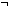 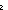 f(inverse(l))) f(inverse(l)))
Def == & ( i:|T|, l1,l2:Edge(T). i:|T|, l1,l2:Edge(T).
Def == & ((l1  to(i)) to(i))
Def == & (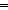 
Def == & ((l2  to(i)) to(i)) 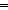  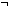 l1 = l2 l1 = l2  IdLnk IdLnk 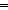  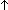 (f(l1)) (f(l1)) 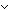 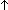 (f(l2))) (f(l2))) |
| | | Thm*  T:(Id T:(Id  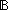 ), to,from:(|T| ), to,from:(|T|  (IdLnk List)), f:(Edge(T) (IdLnk List)), f:(Edge(T)  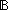 ). ).
Thm* bi-graph(T;to;from) 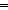  spanner(f;T;to;from) spanner(f;T;to;from)  Prop Prop |
|
| spanner-root | Def spanner-root(f;T;to;from;i) ==  l:Edge(T). (l l:Edge(T). (l  to(i)) to(i)) 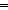  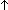 (f(l)) (f(l)) |
|
| bi-graph-edge | Def Edge(G) == {l:IdLnk| 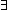 i:|G|. (l i:|G|. (l  from(i)) } from(i)) } |
|
| lconnects | Def lconnects(p;i;j)
Def == lpath(p)
Def == & (||p|| = 0   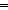  i = j i = j  Id) Id)
Def == & (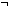 ||p|| = 0 ||p|| = 0   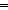  i = source(hd(p)) & j = destination(last(p))) i = source(hd(p)) & j = destination(last(p))) |
| | | Thm*  p:IdLnk List, i,j:Id. lconnects(p;i;j) p:IdLnk List, i,j:Id. lconnects(p;i;j)  Prop Prop |
|
| IdLnk | Def IdLnk == Id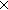 Id Id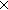 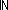 |
| | | Thm* IdLnk  Type Type |
|
| rset | Def |R| == {i:Id| 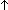 (R(i)) } (R(i)) } |
| | | Thm*  R:(Id R:(Id  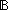 ). |R| ). |R|  Type Type |
|
| Id | Def Id == Atom 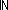 |
| | | Thm* Id  Type Type |
|
| l_member | Def (x  l) == l) == 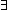 i: i: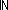 . i<||l|| & x = l[i] . i<||l|| & x = l[i]  T T |
| | | Thm*  T:Type, x:T, l:T List. (x T:Type, x:T, l:T List. (x  l) l)  Prop Prop |