is mentioned by

Thm* E:TaggedEventStruct, tr:|E| List, ls:||tr||. switch_inv(E)(tr) (i,j:||tr||. (i (switchR(tr)^*) ls) (j (switchR(tr)^*) ls) tag(E)(tr[i]) = tag(E)(tr[j]))	[switch_inv_rel_closure]
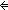Thm* E:TaggedEventStruct, tr:|E| List. switch_inv(E)(tr) (i,j:||tr||. (i switchR(tr) j) tag(E)(tr[i]) = tag(E)(tr[j]))	[switch_inv_rel_same_tag]
Def switch_inv(E)(tr) == i,j,k:||tr||. i < j (is-send(E)(tr[i])) (is-send(E)(tr[j])) tag(E)(tr[i]) = tag(E)(tr[j]) tr[j] delivered at time k (k':||tr||. k' < k & tr[i] delivered at time k' & loc(E)(tr[k']) = loc(E)(tr[k]))	[switch_inv]
Def switch-decomposable(E)(L) == L = nil |E| List (Q:(||L||Prop). (i:||L||. Dec(Q(i))) & (i:||L||. Q(i)) & (i:||L||. Q(i) (is-send(E)(L[i]))) & (i,j:||L||. Q(i) Q(j) tag(E)(L[i]) = tag(E)(L[j])) & (i,j:||L||. Q(i) ij C(Q)(j)))	[switch_decomposable]
Def single-tag-decomposable(E)(L) == L = nil |E| List (L_1,L_2:Trace(E). L = (L_1 @ L_2) |E| List & L_2 = nil |E| List & (xL_1.(yL_2.(x =msg=(E) y))) & (m:Label. (xL_2.tag(E)(x) = m)))	[single_tag_decomposable]
Def Tag-by-msg(E)(tr) == i,j:||tr||. (tr[i] =msg=(E) tr[j]) tag(E)(tr[i]) = tag(E)(tr[j])	[P_tag_by_msg]
Def switch_inv(E; tr) == i,j,k:||tr||. i < j (is-send(E)(tr[i])) (is-send(E)(tr[j])) tag(E)(tr[i]) = tag(E)(tr[j]) (tr[j] =msg=(E) tr[k]) (is-send(E)(tr[k])) (k':||tr||. k' < k & loc(E)(tr[k']) = loc(E)(tr[k]) & (tr[i] =msg=(E) tr[k']) & (is-send(E)(tr[k'])))	[switch_inv2001_03_15_DASH_PM_DASH_12_53_21]

In prior sections: mb structures

Try larger context: GenAutomata