Thm*  E:EventStruct, P:((|E| List)  Prop), A:Type, evt:(A|E|), tg:(ALabel)
, tr:A List.
switchable(E)(P)  
No-dup-send(E)(map(evt;tr))
switch_inv( < A,evt,tg > (E))(tr) (m:Label. P(map(evt; < tr > _m))) P(map(evt;tr)) | [switch_theorem] |
Thm* E:TaggedEventStruct, P:TraceProperty(E).
switchable(E)(P) ((switch_inv(E)  No-dup-send(E)) fuses P) | [switch_inv_theorem2] |
|
Thm* E:TaggedEventStruct, P:TraceProperty(E).
MCS(E)(P)
asyncR(E) preserves P
delayableR(E) preserves P
(P refines (Causal(E) No-dup-deliver(E))) ((switch_inv(E) No-dup-send(E)) fuses P) | [switch_inv_theorem] |
|
Thm* E:TaggedEventStruct, P:TraceProperty(E).
MCS(E)(P)
(P refines (Causal(E) No-dup-deliver(E)))
(((switch_inv(E) AD-normal(E)) No-dup-send(E)) fuses P) | [switch_inv_plus_normal] |
Thm* E:TaggedEventStruct, tr:Trace(E).
(switch_inv(E) No-dup-send(E))(tr)
( tr':Trace(E). switch_inv(E)(tr') & AD-normal(E)(tr') & (tr adR(E) tr')) | [switch_normal_exists] |
|
Thm* E:TaggedEventStruct.
(switch_inv(E) Causal(E) AD-normal(E) No-dup-deliver(E)) refines switch-decomposable(E) | [strong_switch_inv_decomposable] |
Thm* E:TaggedEventStruct, tr:|E| List, ls: ||tr||.
switch_inv(E)(tr)
(i,j:||tr||. (i (switchR(tr)^*) ls) (j (switchR(tr)^*) ls) tag(E)(tr[i]) = tag(E)(tr[j])) | [switch_inv_rel_closure] |
Thm* E:TaggedEventStruct, tr:|E| List.
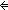switch_inv(E)(tr)  (i,j:||tr||. (i switchR(tr) j) tag(E)(tr[i]) = tag(E)(tr[j])) | [switch_inv_rel_same_tag] |
|
Thm* E:TaggedEventStruct. safetyR(E) preserves switch_inv(E) | [switch_inv_safety] |
Thm* E:TaggedEventStruct, x:|E| List, i:(||x||-1).
switch_inv(E)(x)
 is-send(E)(x[(i+1)])
is-send(E)(x[i])  loc(E)(x[i]) = loc(E)(x[(i+1)]) switch_inv(E)(swap(x;i;i+1)) | [switch_inv_swap] |
|
Def full_switch_inv(E;A;evt;tg;tr_u;tr_l)
== tr_m:A List.
(tr_l R(tg) tr_m) & (map(evt;tr_m) layerR(E) tr_u) & switch_inv( < A,evt,tg > (E))(tr_m) | [full_switch_inv] |
(is-send(E)(tr[i]))