| | Some definitions of interest. |
|
| swap_adjacent | Def swap adjacent[P(x;y)](L1,L2)
Def ==  i: i: (||L1||-1). P(L1[i];L1[(i+1)]) & L2 = swap(L1;i;i+1) (||L1||-1). P(L1[i];L1[(i+1)]) & L2 = swap(L1;i;i+1)  A List A List |
| | | Thm*  A:Type, P:(A A:Type, P:(A  A A  Prop). swap adjacent[P(x,y)] Prop). swap adjacent[P(x,y)]  (A List) (A List)  (A List) (A List)  Prop Prop |
|
| int_seg | Def {i..j } == {k: } == {k: | i | i 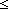 k < j } k < j } |
| | | Thm*  m,n: m,n: . {m..n . {m..n } }  Type Type |
|
| swap | Def swap(L;i;j) == (L o (i, j)) |
| | | Thm*  T:Type, L:T List, i,j: T:Type, L:T List, i,j: ||L||. swap(L;i;j) ||L||. swap(L;i;j)  T List T List |
|
| length | Def ||as|| == Case of as; nil 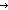 0 ; a.as' 0 ; a.as' 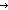 ||as'||+1 (recursive) ||as'||+1 (recursive) |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||   |
| | | Thm* ||nil||   |
|
| not | Def  A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. ( A) A)  Prop Prop |
|
| select | Def l[i] == hd(nth_tl(i;l)) |
| | | Thm*  A:Type, l:A List, n: A:Type, l:A List, n: . 0 . 0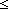 n n   n<||l|| n<||l||   l[n] l[n]  A A |
|
| sym | Def Sym x,y:T. E(x;y) ==  a,b:T. E(a;b) a,b:T. E(a;b)   E(b;a) E(b;a) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). (Sym x,y:T. E(x,y)) Prop). (Sym x,y:T. E(x,y))  Prop Prop |