| 1 | 11. t: S.car
12. mem_f(S.car;t;BL)
13. mem_f(S.car;t;BL)   (
( i: i: ||( ||(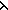 x. < f1(x),( x. < f1(x),(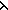 y.S.act(f(y),f1(x)))[ y.S.act(f(y),f1(x)))[ n] > )[ n] > )[ n1]||.
f1(i) = t & mem_f(S.car;s;( n1]||.
f1(i) = t & mem_f(S.car;s;(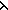 y.S.act(f(y),f1(i)))[ y.S.act(f(y),f1(i)))[ n])) n]))
14. mem_f(S.car;t;BL)   ( ( i: i: ||( ||(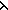 x. < f1(x),( x. < f1(x),(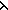 y.S.act(f(y),f1(x)))[ y.S.act(f(y),f1(x)))[ n] > )[ n] > )[ n1]||.
f1(i) = t & mem_f(S.car;s;( n1]||.
f1(i) = t & mem_f(S.car;s;(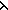 y.S.act(f(y),f1(i)))[ y.S.act(f(y),f1(i)))[ n])) n]))
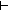  a:Alph. S.act(a,t) = s a:Alph. S.act(a,t) = s |
| 2 | 11. t: S.car
12.  a:Alph. S.act(a,t) = s a:Alph. S.act(a,t) = s
13. mem_f(S.car;t;BL)   (
( i: i: ||( ||(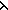 x. < f1(x),( x. < f1(x),(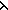 y.S.act(f(y),f1(x)))[ y.S.act(f(y),f1(x)))[ n] > )[ n] > )[ n1]||.
f1(i) = t & mem_f(S.car;s;( n1]||.
f1(i) = t & mem_f(S.car;s;(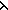 y.S.act(f(y),f1(i)))[ y.S.act(f(y),f1(i)))[ n])) n]))
14. mem_f(S.car;t;BL)   ( ( i: i: ||( ||(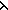 x. < f1(x),( x. < f1(x),(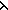 y.S.act(f(y),f1(x)))[ y.S.act(f(y),f1(x)))[ n] > )[ n] > )[ n1]||.
f1(i) = t & mem_f(S.car;s;( n1]||.
f1(i) = t & mem_f(S.car;s;( y.S.act(f(y),f1(i)))[ y.S.act(f(y),f1(i)))[ n])) n]))
 mem_f(S.car;t;BL) mem_f(S.car;t;BL) |