At: mn 23 lem 1 1 1 1 2 1 1 1 2 1
1. Alph: Type
2. R: Alph*
Alph*Prop
3. Fin(Alph)
4. EquivRel x,y:Alph*. x R y
5. Fin(x,y:Alph*//(x R y))
6. 
x,y,z:Alph*. (x R y) 
((z @ x) R (z @ y))
7. g: (x,y:Alph*//(x R y))
8. x: x,y:Alph*//(x R y)
9. y: x,y:Alph*//(x R y)
10. a: Alph
11. p: (x,y:Alph*//(x R y))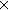
(x,y:Alph*//(x R y))
12. x1: x,y:Alph*//(x R y)
13. y1: x,y:Alph*//(x R y)
14. p = < x1,y1 >
15. y2: Alph*
16. y3: Alph*
17. y2 R y3
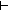(a.y2) R (a.y3)
By:
InstHyp [y2;y3;[a]] 6
THEN
Reduce -1
Generated subgoals:None
About:
