| 1 | 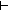  x:((x,y:Alph*//(x R y)) x:((x,y:Alph*//(x R y))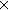 (x,y:Alph*//(x R y))), y:Alph*.
( < (x,y:Alph*//(x R y)) (x,y:Alph*//(x R y))), y:Alph*.
( < (x,y:Alph*//(x R y))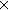 (x,y:Alph*//(x R y)), (x,y:Alph*//(x R y)),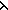 a,p. p/x,y. < a.x,a.y > > :y a,p. p/x,y. < a.x,a.y > > :y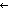 x) = (x/x1,x2. < y@ x) = (x/x1,x2. < y@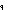 x1,y@ x1,y@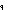 x2 > ) x2 > ) |
| 2 | 12.  x:((x,y:Alph*//(x R y)) x:((x,y:Alph*//(x R y))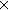 (x,y:Alph*//(x R y))), y:Alph*.
( < (x,y:Alph*//(x R y)) (x,y:Alph*//(x R y))), y:Alph*.
( < (x,y:Alph*//(x R y))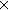 (x,y:Alph*//(x R y)), (x,y:Alph*//(x R y)),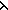 a,p. p/x,y. < a.x,a.y > > :y a,p. p/x,y. < a.x,a.y > > :y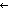 x) = (x/x1,x2. < y@ x) = (x/x1,x2. < y@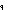 x1,y@ x1,y@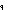 x2 > ) x2 > )
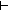 Dec( Dec( x@0:Alph*. (g(x@0@ x@0:Alph*. (g(x@0@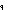 x)) = x)) =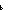 (g(x@0@ (g(x@0@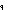 y)) = false y)) = false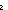 ) ) |