Thm*  r: r:  , s:{s': , s:{s':  | CoPrime(r,s') }, a,b: | CoPrime(r,s') }, a,b: . .
Thm* 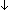  x: x: . ((x = a mod r) & (x = b mod s)) . ((x = a mod r) & (x = b mod s)) | [chrem_exists_a] |
Thm*  r,s: r,s:  . CoPrime(r,s) . CoPrime(r,s)   ( ( a,b: a,b: . .  x: x: . (x = a mod r) & (x = b mod s)) . (x = a mod r) & (x = b mod s)) | [chrem_exists] |
Thm*  r: r:  , s:{s': , s:{s':  | CoPrime(r,s') }. | CoPrime(r,s') }. 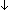  x: x: . ((x = 1 mod r) & (x = 0 mod s)) . ((x = 1 mod r) & (x = 0 mod s)) | [chrem_exists_aux_a] |
Thm*  r,s: r,s:  . CoPrime(r,s) . CoPrime(r,s)   ( ( x: x: . (x = 1 mod r) & (x = 0 mod s)) . (x = 1 mod r) & (x = 0 mod s)) | [chrem_exists_aux] |
Thm*  p: p: . prime(p) . prime(p)    p = 0 & p = 0 &  (p ~ 1) & ( (p ~ 1) & ( a: a: . a | p . a | p   (a ~ 1) (a ~ 1) 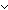 (a ~ p)) (a ~ p)) | [prime_elim] |
Thm*  a: a: . atomic(a) . atomic(a)    (a ~ 1) & ( (a ~ 1) & ( b: b: . b | a . b | a   (b ~ 1) (b ~ 1) 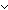 (b ~ a)) (b ~ a)) | [atomic_char] |
Thm*  a,b: a,b: . .  y: y: . GCD(a;b;y) & gcd(a;b) = y . GCD(a;b;y) & gcd(a;b) = y | [gcd_elim] |
Thm*  a,b,c,x,y: a,b,c,x,y: . .
Thm* GCD(a;b;x)
Thm*  
Thm* GCD(x;c;y)
Thm*  
Thm* y | a & y | b & y | c & ( z: z: . z | a . z | a   z | b z | b   z | c z | c   z | y) z | y) | [gcd_of_triple] |
Thm*  a: a: , b: , b:  . a | b & . a | b &  b | a b | a   a<b & a | b a<b & a | b | [pdivisor_bound] |
Thm*  a,b: a,b: . a | b & b | a . a | b & b | a   a = a = 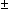 b b | [assoc_reln] |
Def prime(a) ==  a = 0 & a = 0 &  (a ~ 1) & ( (a ~ 1) & ( b,c: b,c: . a | b . a | b c c   a | b a | b 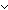 a | c) a | c) | [prime] |
Def atomic(a) ==  a = 0 & a = 0 &  (a ~ 1) & (a ~ 1) &  reducible(a) reducible(a) | [atomic] |
Def reducible(a) ==  b,c: b,c:  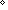 . .  (b ~ 1) & (b ~ 1) &  (c ~ 1) & a = b (c ~ 1) & a = b c c | [reducible] |
Def GCD(a;b;y) == y | a & y | b & ( z: z: . z | a & z | b . z | a & z | b   z | y) z | y) | [gcd_p] |
| Def a ~ b == a | b & b | a | [assoced] |