Selected Objects
| COM | binrel_com |
BINARY RELATIONS
... |
| def | refl |
Refl(T;x,y.E(x;y)) ==  a:T. E(a;a) a:T. E(a;a) |
| THM | refl_functionality_wrt_iff |
 R,R':(T R,R':(T  T T  Prop). Prop).
( x,y:T. R(x,y) x,y:T. R(x,y)   R'(x,y)) R'(x,y))   (Refl(T;x,y.R(x,y)) (Refl(T;x,y.R(x,y))   Refl(T;x,y.R'(x,y))) Refl(T;x,y.R'(x,y))) |
| def | sym |
Sym x,y:T. E(x;y) ==  a,b:T. E(a;b) a,b:T. E(a;b)   E(b;a) E(b;a) |
| THM | sym_functionality_wrt_iff |
 R,R':(T R,R':(T  T T  Prop). Prop).
( x,y:T. R(x,y) x,y:T. R(x,y)   R'(x,y)) R'(x,y))   ((Sym x,y:T. R(x,y)) ((Sym x,y:T. R(x,y))   (Sym x,y:T. R'(x,y))) (Sym x,y:T. R'(x,y))) |
| def | trans |
Trans x,y:T. E(x;y) ==  a,b,c:T. E(a;b) a,b,c:T. E(a;b)   E(b;c) E(b;c)   E(a;c) E(a;c) |
| THM | trans_functionality_wrt_iff |
 R,R':(T R,R':(T  T T  Prop). Prop).
( x,y:T. R(x,y) x,y:T. R(x,y)   R'(x,y)) R'(x,y))   ((Trans y,x:T. R(x,y)) ((Trans y,x:T. R(x,y))   (Trans y,x:T. R'(x,y))) (Trans y,x:T. R'(x,y))) |
| THM | trans_rel_self_functionality |
 R:(T R:(T  T T  Prop). Prop).
(Trans x,y:T. R(x,y))
 
( a,a',b,b':T. R(b,a) a,a',b,b':T. R(b,a)   R(a',b') R(a',b')   R(a,a') R(a,a')   R(b,b')) R(b,b')) |
| def | equiv_rel |
EquivRel x,y:T. E(x;y)
== Refl(T;x,y.E(x;y)) & (Sym x,y:T. E(x;y)) & (Trans x,y:T. E(x;y)) |
| THM | equiv_rel_subtyping |
 R:(T R:(T  T T  Type), Q:(T Type), Q:(T  Prop). Prop).
(EquivRel x,y:T. R(x,y))   (EquivRel x,y:{z:T| Q(z) }. R(x,y)) (EquivRel x,y:{z:T| Q(z) }. R(x,y)) |
| def | preorder |
Preorder(T;x,y.R(x;y)) == Refl(T;x,y.R(x;y)) & (Trans x,y:T. R(x;y)) |
| def | symmetrize |
Symmetrize(x,y.R(x;y);a;b) == R(a;b) & R(b;a) |
| THM | symmetrized_preorder |
 R:(T R:(T  T T  Prop). Prop).
Preorder(T;x,y.R(x,y))   (EquivRel a,b:T. Symmetrize(x,y.R(x,y);a;b)) (EquivRel a,b:T. Symmetrize(x,y.R(x,y);a;b)) |
| THM | trans_rel_func_wrt_sym_self |
 R:(T R:(T  T T  Prop). Prop).
(Trans x,y:T. R(x,y))
 
( a,a',b,b':T. a,a',b,b':T.
(Symmetrize(x,y.R(x,y);a;b)
( 
(Symmetrize(x,y.R(x,y);a';b')   (R(a,a') (R(a,a')   R(b,b'))) R(b,b'))) |
| THM | equiv_rel_iff |
EquivRel A,B:Prop. A   B B |
| THM | equiv_rel_functionality_wrt_iff |
 E:(T E:(T  T T  Prop), E':(T' Prop), E':(T'  T' T'  Prop). Prop).
T = T'
 
( x,y:T. E(x,y) x,y:T. E(x,y)   E'(x,y)) E'(x,y))
 
((EquivRel x,y:T. E(x,y))   (EquivRel x,y:T'. E'(x,y))) (EquivRel x,y:T'. E'(x,y))) |
| COM | equiv_rel_self_fun_com |
This lemma is useful for quickly proving functionalitylemmas for equivalence relations. |
| THM | equiv_rel_self_functionality |
 R:(T R:(T  T T  Prop). Prop).
(EquivRel x,y:T. R(x,y))
 
( a,a',b,b':T. R(a,b) a,a',b,b':T. R(a,b)   R(a',b') R(a',b')   (R(a,a') (R(a,a')   R(b,b'))) R(b,b'))) |
| THM | squash_thru_equiv_rel |
 E:(T E:(T  T T  Prop). Prop). 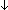 (EquivRel x,y:T. E(x,y)) (EquivRel x,y:T. E(x,y))   (EquivRel x,y:T. (EquivRel x,y:T. 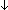 E(x,y)) E(x,y)) |
| def | eqfun_p |
IsEqFun(T;eq) ==  x,y:T. x,y:T. 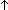 (x eq y) (x eq y)   x = y x = y |
| THM | sq_stable__eqfun_p |
 eq:(T eq:(T  T T  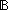 ). SqStable(IsEqFun(T;eq)) ). SqStable(IsEqFun(T;eq)) |
| def | anti_sym |
AntiSym(T;x,y.R(x;y)) ==  x,y:T. R(x;y) x,y:T. R(x;y)   R(y;x) R(y;x)   x = y x = y |
| THM | anti_sym_functionality_wrt_iff |
 R,R':(T R,R':(T  T T  Prop). Prop).
( x,y:T. R(x,y) x,y:T. R(x,y)   R'(x,y)) R'(x,y))   (AntiSym(T;x,y.R(x,y)) (AntiSym(T;x,y.R(x,y))   AntiSym(T;x,y.R'(x,y))) AntiSym(T;x,y.R'(x,y))) |
| def | st_anti_sym |
StAntiSym(T;x,y.R(x;y)) ==  x,y:T. x,y:T. 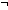 (R(x;y) & R(y;x)) (R(x;y) & R(y;x)) |
| def | strict_part |
strict_part(x,y.R(x;y);a;b) == R(a;b) & 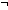 R(b;a) R(b;a) |
| THM | strict_part_irrefl |
 R:(T R:(T  T T  Prop), a,b:T. strict_part(x,y.R(x,y);a;b) Prop), a,b:T. strict_part(x,y.R(x,y);a;b)   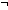 a = b a = b |
| def | connex |
Connex(T;x,y.R(x;y)) ==  x,y:T. R(x;y) x,y:T. R(x;y) 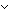 R(y;x) R(y;x) |
| THM | connex_functionality_wrt_iff |
 R,R':(T R,R':(T  T T  Prop). Prop).
( x,y:T. R(x,y) x,y:T. R(x,y)   R'(x,y)) R'(x,y))   (Connex(T;x,y.R(x,y)) (Connex(T;x,y.R(x,y))   Connex(T;x,y.R'(x,y))) Connex(T;x,y.R'(x,y))) |
| THM | connex_functionality_wrt_implies |
 R,R':(T R,R':(T  T T  Prop). Prop).
( x,y:T. R(x,y) x,y:T. R(x,y)   R'(x,y)) R'(x,y))   Connex(T;x,y.R(x,y)) Connex(T;x,y.R(x,y))   Connex(T;x,y.R'(x,y)) Connex(T;x,y.R'(x,y)) |
| THM | connex_iff_trichot |
 R:(T R:(T  T T  Prop). Prop).
( a,b:T. Dec(R(a,b))) a,b:T. Dec(R(a,b)))
 
(Connex(T;x,y.R(x,y))
( 
(( a,b:T. a,b:T.
((strict_part(x,y.R(x,y);a;b)
((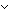 Symmetrize(x,y.R(x,y);a;b) Symmetrize(x,y.R(x,y);a;b)
((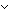 strict_part(x,y.R(x,y);b;a))) strict_part(x,y.R(x,y);b;a))) |
| def | order |
Order(T;x,y.R(x;y))
== Refl(T;x,y.R(x;y)) & (Trans x,y:T. R(x;y)) & AntiSym(T;x,y.R(x;y)) |
| THM | order_functionality_wrt_iff |
 R,R':(T R,R':(T  T T  Prop). Prop).
( x,y:T. R(x,y) x,y:T. R(x,y)   R'(x,y)) R'(x,y))   (Order(T;x,y.R(x,y)) (Order(T;x,y.R(x,y))   Order(T;x,y.R'(x,y))) Order(T;x,y.R'(x,y))) |
| def | linorder |
Linorder(T;x,y.R(x;y)) == Order(T;x,y.R(x;y)) & Connex(T;x,y.R(x;y)) |
| THM | linorder_functionality_wrt_iff |
 R,R':(T R,R':(T  T T  Prop). Prop).
( x,y:T. R(x,y) x,y:T. R(x,y)   R'(x,y)) R'(x,y))
 
(Linorder(T;x,y.R(x,y))   Linorder(T;x,y.R'(x,y))) Linorder(T;x,y.R'(x,y))) |
| THM | order_split |
 R:(T R:(T  T T  Prop). Prop).
Order(T;x,y.R(x,y))
 
( x,y:T. Dec(x = y)) x,y:T. Dec(x = y))   ( ( a,b:T. R(a,b) a,b:T. R(a,b)   strict_part(x,y.R(x,y);a;b) strict_part(x,y.R(x,y);a;b) 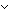 a = b) a = b) |
| def | irrefl |
Irrefl(T;x,y.E(x;y)) ==  a:T. a:T. 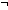 E(a;a) E(a;a) |
| THM | trans_imp_sp_trans |
 R:(T R:(T  T T  Prop). Prop).
(Trans a,b:T. R(a,b))   (Trans a,b:T. strict_part(x,y.R(x,y);a;b)) (Trans a,b:T. strict_part(x,y.R(x,y);a;b)) |
| THM | trans_imp_sp_trans_a |
 R:(T R:(T  T T  Prop). Prop).
(Trans a,b:T. R(a,b))
 
( a,b,c:T. R(a,b) a,b,c:T. R(a,b)   strict_part(x,y.R(x,y);b;c) strict_part(x,y.R(x,y);b;c)   strict_part(x,y.R(x,y);a;c)) strict_part(x,y.R(x,y);a;c)) |
| THM | trans_imp_sp_trans_b |
 R:(T R:(T  T T  Prop). Prop).
(Trans a,b:T. R(a,b))
 
( a,b,c:T. strict_part(x,y.R(x,y);a;b) a,b,c:T. strict_part(x,y.R(x,y);a;b)   R(b,c) R(b,c)   strict_part(x,y.R(x,y);a;c)) strict_part(x,y.R(x,y);a;c)) |
| THM | linorder_le_neg |
 R:(T R:(T  T T  Prop). Prop).
Linorder(T;x,y.R(x,y))   ( ( a,b:T. a,b:T. 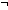 R(a,b) R(a,b)   strict_part(x,y.R(x,y);b;a)) strict_part(x,y.R(x,y);b;a)) |
| THM | linorder_lt_neg |
 R:(T R:(T  T T  Prop). Prop).
( x,y:T. Dec(R(x,y))) x,y:T. Dec(R(x,y)))
 
Linorder(T;x,y.R(x,y))   ( ( a,b:T. a,b:T. 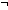 strict_part(x,y.R(x,y);a;b) strict_part(x,y.R(x,y);a;b)   R(b,a)) R(b,a)) |