| 1 | 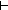 ( (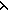 x.f(x)) x.f(x)) 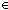 (x,y:A//(x R_f y)) (x,y:A//(x R_f y))  (x,y:B//(x R y)) (x,y:B//(x R y)) |
| 2 | 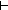 (x,y:A//(x R_f y)) (x,y:A//(x R_f y))  (x,y:B//(x R y)) (x,y:B//(x R y)) 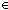 Type{[1 | i 0]} Type{[1 | i 0]} |
| 3 | 10. F: (x,y:A//(x R_f y))  (x,y:B//(x R y)) (x,y:B//(x R y))
11. F = (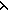 x.f(x)) x.f(x))
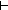 g g 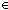 (x,y:B//(x R y)) (x,y:B//(x R y))  (x,y:A//(x R_f y)) (x,y:A//(x R_f y)) |
| 4 | 10. F: (x,y:A//(x R_f y))  (x,y:B//(x R y)) (x,y:B//(x R y))
11. F = (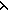 x.f(x)) x.f(x))
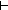 (x,y:B//(x R y)) (x,y:B//(x R y))  (x,y:A//(x R_f y)) (x,y:A//(x R_f y)) 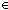 Type{[1 | i 0]} Type{[1 | i 0]} |
| 5 | 10. F: (x,y:A//(x R_f y))  (x,y:B//(x R y)) (x,y:B//(x R y))
11. F = (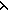 x.f(x)) x.f(x))
12. G: (x,y:B//(x R y))  (x,y:A//(x R_f y)) (x,y:A//(x R_f y))
13. G = g 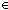 (x,y:B//(x R y)) (x,y:B//(x R y))  (x,y:A//(x R_f y)) (x,y:A//(x R_f y))
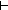 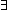 F:((x,y:A//(x R_f y)) F:((x,y:A//(x R_f y))  (x,y:B//(x R y))). Bij(x,y:A//(x R_f y); x,y:B//(x R y); F) (x,y:B//(x R y))). Bij(x,y:A//(x R_f y); x,y:B//(x R y); F) |