---

Step * 1 3 2 of Lemma aa_kleene_fan_contra_partial_imax


1. f :     bar()@i
2. b:  bar(). a:. ((f a) = b)@i
3. T :       @i
4. indx,input:.
     ((nsteps:. (((T indx input nsteps))  (f indx input)))
      ((f indx input)  (nsteps:. ((T indx input nsteps))))
      (n1,n2:.  (((n1  n2)  ((T indx input n1)))  ((T indx input n2)))))@i
5. x : @i
6. y.if T y y x then 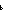(f y y) else ff fi     
 l: List
   ((x = ||l||)
    ((l.y:
            ((y < ||l||)
             (((((T y y ||l||))  f y y = ff)  l[y] = tt)  ((((T y y ||l||))  f y y = tt)  l[y] = ff)))) 
      l))
BY
{ ((Reduce 0
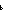    THEN (InstLemma `mklist_length` [y.if T y y x then (f y y) else ff fi ;x]
          THEN Auto
          THEN (Assert ||mklist(x;y.if T y y x then 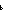(f y y) else ff fi )|| = x BY
                      MaAuto))
    )
   THEN InstConcl [mklist(x;y.if T y y x then 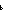(f y y) else ff fi )]
   THEN Auto
   THEN Try (Complete ((Termination THEN Auto)))) }

1
1. f :     bar()@i
2. b:  bar(). a:. ((f a) = b)@i
3. T :       @i
4. indx,input:.
     ((nsteps:. (((T indx input nsteps))  (f indx input)))
      ((f indx input)  (nsteps:. ((T indx input nsteps))))
      (n1,n2:.  (((n1  n2)  ((T indx input n1)))  ((T indx input n2)))))@i
5. x : @i
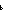6. y.if T y y x then (f y y) else ff fi     
7. ||mklist(x;y.if T y y x then 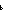(f y y) else ff fi )|| ~ x
8. ||mklist(x;y.if T y y x then 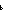(f y y) else ff fi )|| = x
9. y : @i
10. y < ||mklist(x;y.if T y y x then 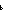(f y y) else ff fi )||@i
11. (T y y ||mklist(x;y.if T y y x then 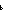(f y y) else ff fi )||)@i
12. f y y = ff@i
 mklist(x;y.if T y y x then 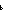(f y y) else ff fi )[y] = tt

2
1. f :     bar()@i
2. b:  bar(). a:. ((f a) = b)@i
3. T :       @i
4. indx,input:.
     ((nsteps:. (((T indx input nsteps))  (f indx input)))
      ((f indx input)  (nsteps:. ((T indx input nsteps))))
      (n1,n2:.  (((n1  n2)  ((T indx input n1)))  ((T indx input n2)))))@i
5. x : @i
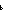6. y.if T y y x then (f y y) else ff fi     
7. ||mklist(x;y.if T y y x then 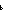(f y y) else ff fi )|| ~ x
8. ||mklist(x;y.if T y y x then 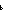(f y y) else ff fi )|| = x
9. y : @i
10. y < ||mklist(x;y.if T y y x then 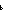(f y y) else ff fi )||@i
11. (T y y ||mklist(x;y.if T y y x then 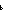(f y y) else ff fi )||)@i
12. f y y = tt@i
 mklist(x;y.if T y y x then 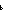(f y y) else ff fi )[y] = ff



1.  f  :  \mBbbN{}  {}\mrightarrow{}  \mBbbN{}  {}\mrightarrow{}  bar(\mBbbB{})@i
2.  \mforall{}b:\mBbbN{}  {}\mrightarrow{}  bar(\mBbbB{}).  \mexists{}a:\mBbbN{}.  ((f  a)  =  b)@i
3.  T  :  \mBbbN{}  {}\mrightarrow{}  \mBbbN{}  {}\mrightarrow{}  \mBbbN{}  {}\mrightarrow{}  \mBbbB{}@i
4.  \mforall{}indx,input:\mBbbN{}.
          ((\mforall{}nsteps:\mBbbN{}.  ((\muparrow{}(T  indx  input  nsteps))  {}\mRightarrow{}  (f  indx  input)\mdownarrow{}))
          \mwedge{}  ((f  indx  input)\mdownarrow{}  {}\mRightarrow{}  (\mexists{}nsteps:\mBbbN{}.  (\muparrow{}(T  indx  input  nsteps))))
          \mwedge{}  (\mforall{}n1,n2:\mBbbN{}.    (((n1  \mleq{}  n2)  \mwedge{}  (\muparrow{}(T  indx  input  n1)))  {}\mRightarrow{}  (\muparrow{}(T  indx  input  n2)))))@i
5.  x  :  \mBbbN{}@i
6.  \mlambda{}y.if  T  y  y  x  then  \mneg{}\msubb{}(f  y  y)  else  ff  fi    \mmember{}  \mBbbN{}  {}\mrightarrow{}  \mBbbB{}
\mvdash{}  \mexists{}l:\mBbbB{}  List
      ((x  =  ||l||)
      \mwedge{}  ((\mlambda{}l.\mforall{}y:\mBbbN{}
                        ((y  <  ||l||)
                        {}\mRightarrow{}  ((((\muparrow{}(T  y  y  ||l||))  \mwedge{}  f  y  y  =  ff)  {}\mRightarrow{}  l[y]  =  tt)
                              \mwedge{}  (((\muparrow{}(T  y  y  ||l||))  \mwedge{}  f  y  y  =  tt)  {}\mRightarrow{}  l[y]  =  ff)))) 
            l))


By

((Reduce  0
    THEN  (InstLemma  `mklist\_length`  [\mkleeneopen{}\mlambda{}y.if  T  y  y  x  then  \mneg{}\msubb{}(f  y  y)  else  ff  fi  \mkleeneclose{};\mkleeneopen{}x\mkleeneclose{}]\mcdot{}
                THEN  Auto
                THEN  (Assert  ||mklist(x;\mlambda{}y.if  T  y  y  x  then  \mneg{}\msubb{}(f  y  y)  else  ff  fi  )||  =  x  BY
                                        MaAuto))\mcdot{}
    )
  THEN  InstConcl  [\mkleeneopen{}mklist(x;\mlambda{}y.if  T  y  y  x  then  \mneg{}\msubb{}(f  y  y)  else  ff  fi  )\mkleeneclose{}]\mcdot{}
  THEN  Auto
  THEN  Try  (Complete  ((Termination  THEN  Auto))))\mcdot{}



Home Index