Nuprl Lemma : hw5_7_2
T:Type. eq:T 
T 
. addp:T T T . zero:T .
(((x,y:T.
((
z:T. (
(addp x y z)))
(xp,yp,zp,z:T. ((((eq x xp)) ((eq y yp)) ((addp xp yp zp)) ((addp x y z))) 
((eq z zp))))))
(x,y,z,t1,t2,r:T. ((((addp x y t1)) ((addp t1 z r)) ((addp y z t2))) ((addp t2 x r))))
(x,y,z:T. (((addp x y z)) ((addp y x z))))
((u:T. ((zero u))) (u,x:T. (((zero u)) (((addp x u x)) ((addp u x x))))))
EquivRel(T;x,y.(eq x y))
(u:T. (((zero u)) (x:T. xi:T. ((addp x xi u)))))
(x,y:T. (((eq x y)) ((zero x) 
(zero y)))))
(x,y,z:T. ((((addp x y z)) ((eq z x))) ((zero y)))))
Proof
Definitions occuring in Statement :
equiv_rel: EquivRel(T;x,y.E[x; y]),
assert: b,
bool: ,
all: x:A. B[x],
exists: x:A. B[x],
iff: P Q,
implies: P Q,
and: P Q,
apply: f a,
function: x:A B[x],
universe: Type
Definitions :
all: x:A. B[x],
implies: P Q,
and: P Q,
exists: x:A. B[x],
iff: P Q,
member: t 
T,
prop: 
,
so_lambda: 
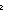x.t[x],
so_lambda: 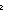x y.t[x; y],
rev_implies: P Q,
uall: [x:A]. B[x],
so_apply: x[s],
so_apply: x[s1;s2],
equiv_rel: EquivRel(T;x,y.E[x; y]),
refl: Refl(T;x,y.E[x; y]),
sym: Sym(T;x,y.E[x; y]),
guard: {T}
Lemmas :
assert_wf,
all_wf,
exists_wf,
equiv_rel_wf,
iff_wf,
bool_wf
\mforall{}T:Type. \mforall{}eq:T {}\mrightarrow{} T {}\mrightarrow{} \mBbbB{}. \mforall{}addp:T {}\mrightarrow{} T {}\mrightarrow{} T {}\mrightarrow{} \mBbbB{}. \mforall{}zero:T {}\mrightarrow{} \mBbbB{}.
(((\mforall{}x,y:T.
((\mexists{}z:T. (\muparrow{}(addp x y z)))
\mwedge{} (\mforall{}xp,yp,zp,z:T.
(((\muparrow{}(eq x xp)) \mwedge{} (\muparrow{}(eq y yp)) \mwedge{} (\muparrow{}(addp xp yp zp)) \mwedge{} (\muparrow{}(addp x y z)))
{}\mRightarrow{} (\muparrow{}(eq z zp))))))
\mwedge{} (\mforall{}x,y,z,t1,t2,r:T.
(((\muparrow{}(addp x y t1)) \mwedge{} (\muparrow{}(addp t1 z r)) \mwedge{} (\muparrow{}(addp y z t2))) {}\mRightarrow{} (\muparrow{}(addp t2 x r))))
\mwedge{} (\mforall{}x,y,z:T. ((\muparrow{}(addp x y z)) {}\mRightarrow{} (\muparrow{}(addp y x z))))
\mwedge{} ((\mexists{}u:T. (\muparrow{}(zero u))) \mwedge{} (\mforall{}u,x:T. ((\muparrow{}(zero u)) {}\mRightarrow{} ((\muparrow{}(addp x u x)) \mwedge{} (\muparrow{}(addp u x x))))))
\mwedge{} EquivRel(T;x,y.\muparrow{}(eq x y))
\mwedge{} (\mforall{}u:T. ((\muparrow{}(zero u)) {}\mRightarrow{} (\mforall{}x:T. \mexists{}xi:T. (\muparrow{}(addp x xi u)))))
\mwedge{} (\mforall{}x,y:T. ((\muparrow{}(eq x y)) {}\mRightarrow{} (\muparrow{}(zero x) \mLeftarrow{}{}\mRightarrow{} \muparrow{}(zero y)))))
{}\mRightarrow{} (\mforall{}x,y,z:T. (((\muparrow{}(addp x y z)) \mwedge{} (\muparrow{}(eq z x))) {}\mRightarrow{} (\muparrow{}(zero y)))))
Date html generated:
2013_03_20-AM-09_55_18
Last ObjectModification:
2012_11_27-AM-10_33_34
Home
Index