Step
*
1
2
1
of Lemma
not_base_decidable_eq_weaker
1. ( t:Base. ((
t:Base. ((
 (t)
(t) )
) 
 (t)
(t) ))
)) 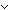 (
( t:Base. ((
t:Base. (( (t ~ bottom()))
(t ~ bottom())) 
 (t)
(t) ))@i
))@i
2.  t1,t2:Base. Dec(t1 = t2)@i
t1,t2:Base. Dec(t1 = t2)@i
3. t : Base@i
 (t)
(t)
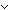 (
( (t)
(t) )
)
BY
{ (InstHyp [ t
t ;
; bottom()
bottom() ] 2
] 2
THEN Auto
THEN (Unfold `decidable` (-1) THEN (Assert  t:Base. ((t)
t:Base. ((t)

 ) BY MaAuto))
) BY MaAuto))
THEN (Assert  t:Base. ((t = bottom())
t:Base. ((t = bottom()) 
 (
( (t)
(t) )) BY
)) BY
(Auto THEN HypSubst (-1) 0 THEN Auto THEN BLemma `bottom_diverge`))) }
1
1. ( t:Base. ((
t:Base. ((
 (t)
(t) )
) 
 (t)
(t) ))
)) 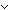 (
( t:Base. ((
t:Base. (( (t ~ bottom()))
(t ~ bottom())) 
 (t)
(t) ))@i
))@i
2.  t1,t2:Base. Dec(t1 = t2)@i
t1,t2:Base. Dec(t1 = t2)@i
3. t : Base@i
4. (t = bottom()) 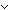 (
( (t = bottom()))
(t = bottom()))
5.  t:Base. ((t)
t:Base. ((t)

 )
)
6.  t:Base. ((t = bottom())
t:Base. ((t = bottom()) 
 (
( (t)
(t) ))
))
 (t)
(t)
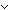 (
( (t)
(t) )
)
1. (\mforall{}t:Base. ((\mneg{}\mneg{}(t)\mdownarrow{}) {}\mRightarrow{} (t)\mdownarrow{})) \mvee{} (\mforall{}t:Base. ((\mneg{}(t \msim{} bottom())) {}\mRightarrow{} (t)\mdownarrow{}))@i
2. \mforall{}t1,t2:Base. Dec(t1 = t2)@i
3. t : Base@i
\mvdash{} (t)\mdownarrow{} \mvee{} (\mneg{}(t)\mdownarrow{})
By
(InstHyp [\mkleeneopen{}t\mkleeneclose{};\mkleeneopen{}bottom()\mkleeneclose{}] 2\mcdot{}
THEN Auto
THEN (Unfold `decidable` (-1) THEN (Assert \mforall{}t:Base. ((t)\mdownarrow{} \mmember{} \mBbbP{}) BY MaAuto))
THEN (Assert \mforall{}t:Base. ((t = bottom()) {}\mRightarrow{} (\mneg{}(t)\mdownarrow{})) BY
(Auto THEN HypSubst (-1) 0 THEN Auto THEN BLemma `bottom\_diverge`)))
Home
Index