Nuprl Lemma : spr_down_closed
g:
List 
. (spr(g) 
(a: List. s:. (((g (a @ [s])) = 0) ((g a) = 0))))
Proof
Definitions occuring in Statement :
append: as @ bs,
nat: ,
all: x:A. B[x],
implies: P Q,
apply: f a,
function: x:A B[x],
natural_number: $n,
equal: s = t
Definitions :
false: False,
not: 
A,
le: A 
B,
member: t 
T,
implies: P Q,
nat: ,
all: x:A. B[x],
so_lambda: 
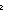x.t[x],
true: True,
squash: 
T,
uall: [x:A]. B[x],
prop: 
,
spr: spr(g),
and: P 
Q,
so_apply: x[s],
guard: {T},
gt: i > j
Lemmas :
spr_wf,
Error :list_wf,
le_wf,
Error :nil_wf,
Error :cons_wf,
append_wf,
nat_wf,
equal_wf,
all_wf,
subtype_rel_set_simple,
gt_wf,
contrapos1
\mforall{}g:\mBbbN{} List {}\mrightarrow{} \mBbbN{}. (spr(g) {}\mRightarrow{} (\mforall{}a:\mBbbN{} List. \mforall{}s:\mBbbN{}. (((g (a @ [s])) = 0) {}\mRightarrow{} ((g a) = 0))))
Date html generated:
2013_03_20-AM-10_32_24
Last ObjectModification:
2013_03_07-PM-08_16_31
Home
Index