Step
*
1
2
1
1
1
1
1
of Lemma
seg_sum_shift
1. p : 
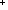 @i
@i
2. 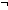 (p
(p 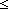 0)
0)
3. q : 
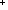 @i
@i
4. L : 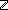 List@i
List@i
5. x : 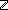
6. x = seg_sum(p - 1;q - 1;tl(L))
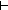 l_sum(firstn((q + 1) - p;nth_tl(p - 1;tl(L)))) = x
l_sum(firstn((q + 1) - p;nth_tl(p - 1;tl(L)))) = x
BY
{ Assert 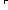 ((q + 1) - p) = (((q - 1) + 1) - p - 1)
((q + 1) - p) = (((q - 1) + 1) - p - 1)
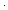 }
}
1
.....assertion.....
1. p : 
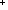 @i
@i
2. 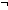 (p
(p 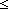 0)
0)
3. q : 
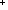 @i
@i
4. L : 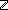 List@i
List@i
5. x : 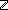
6. x = seg_sum(p - 1;q - 1;tl(L))
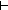 ((q + 1) - p) = (((q - 1) + 1) - p - 1)
((q + 1) - p) = (((q - 1) + 1) - p - 1)
2
1. p : 
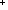 @i
@i
2. 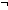 (p
(p 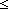 0)
0)
3. q : 
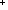 @i
@i
4. L : 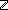 List@i
List@i
5. x : 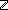
6. x = seg_sum(p - 1;q - 1;tl(L))
7. ((q + 1) - p) = (((q - 1) + 1) - p - 1)
 l_sum(firstn((q + 1) - p;nth_tl(p - 1;tl(L)))) = x
l_sum(firstn((q + 1) - p;nth_tl(p - 1;tl(L)))) = x
Latex:
1. p : \mBbbN{}\msupplus{}@i
2. \mneg{}(p \mleq{} 0)
3. q : \mBbbN{}\msupplus{}@i
4. L : \mBbbZ{} List@i
5. x : \mBbbZ{}
6. x = seg\_sum(p - 1;q - 1;tl(L))
\mvdash{} l\_sum(firstn((q + 1) - p;nth\_tl(p - 1;tl(L)))) = x
By
Assert \mkleeneopen{}((q + 1) - p) = (((q - 1) + 1) - p - 1)\mkleeneclose{}\mcdot{}
Home
Index