Nuprl Lemma : vr_rsub_to_sub
n,m:
. (m - n ~ m - n)
Proof not projected
Definitions occuring in Statement :
all: x:A. B[x],
subtract: n - m,
int: ,
sqequal: s ~ t,
rsub: x - y
Definitions :
CollapseTHEN: Error :CollapseTHEN,
Unfold: Error :Unfold,
uall: [x:A]. B[x],
function: x:A 
B[x],
all: x:A. B[x],
sqequal: s ~ t,
not: 
A,
less_than: a < b,
isect: 
x:A. B[x],
uimplies: b supposing a,
product: x:A 
B[x],
and: P 
Q,
uiff: uiff(P;Q),
int: ,
subtype_rel: A 
r B,
tunion: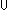 
x:A.B[x],
b-union: A 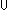B,
real: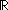 
,
sq_type: SQType(T),
rsub: x - y,
ge: i 
j ,
le: A 
B,
strong-subtype: strong-subtype(A;B),
member: t 
T,
equal: s = t,
radd: r + s,
rminus: -(r),
tactic: Error :tactic,
callbyvalue: callbyvalue,
ifthenelse: if b then t else f fi ,
is-rational: is-rational(r),
spread: spread def,
outl: outl(x),
inl: inl x ,
pair: <a, b>,
lambda: 
x.A[x],
apply: f a,
qmul: r * s,
minus: -n,
natural_number: $n,
Auto: Error :Auto,
value-type: value-type(T),
qadd: r + s,
inf-add: x + y,
subtract: n - m,
rationals: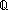 
,
union: left + right,
quotient: x,y:A//B[x; y],
bfalse: ff,
btrue: tt,
ispair: ispair(z;a;b),
isint: isint(z;a;b),
bor: p 
q,
multiply: n * m,
callbyvalueall: callbyvalueall,
base: Base,
guard: {T},
implies: P 
Q,
add: n + m,
fpf: a:A fp-> B[a],
eclass: EClass(A[eo; e]),
MaAuto: Error :MaAuto,
has-value: has-value(a),
subtype: S T,
so_lambda: 
x.t[x],
set: {x:A| B[x]} ,
qle: r s,
nat: 
,
infinitesmal: Infinitesmal,
void: Void,
universe: Type,
bool: 
,
Id: Id,
atom: Atom$n
Lemmas :
Id_wf,
Id-has-value,
real-has-value,
rational-is-real,
bool_wf,
tunion_wf,
member_wf,
qle_wf,
infinitesmal_wf,
nat_wf,
subtract-elim,
int_subtype_base,
rationals_wf,
ifthenelse_wf,
qadd_wf,
qmul_wf,
int-value-type,
value-type_wf,
subtype_base_sq,
real_wf,
rsub_wf
\mforall{}n,m:\mBbbZ{}. (m - n \msim{} m - n)
Date html generated:
2012_02_20-PM-03_32_23
Last ObjectModification:
2012_02_02-PM-01_55_06
Home
Index