| | Some definitions of interest. |
|
| hanoi_seq | Def s is a Hanoi(n disk) seq on a..z
Def ==  x,x':{a...z}. x,x':{a...z}.
Def == x+1 = x'   ( ( k:{1...n}. Moving disk k of n takes s(x) to s(x')) k:{1...n}. Moving disk k of n takes s(x) to s(x')) |
| | | Thm*  n: n: , a,z: , a,z: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* s is a Hanoi(n disk) seq on a..z  Prop Prop |
|
| hanoi_PEG | Def Peg == {1...3} |
| | | Thm* Peg  Type Type |
|
| hanoi_peg_perm | Def permute(p to r ; q to s)(u) == if u=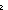 p p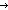 r ; u= r ; u=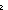 q q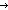 s else otherPeg(r; s) fi s else otherPeg(r; s) fi |
| | | Thm*  p,r,q,s:Peg. p p,r,q,s:Peg. p  q q   r r  s s   permute(p to r ; q to s) permute(p to r ; q to s)  Peg Peg  Peg Peg |
|
| hanoi_otherpeg | Def otherPeg(x; y) == 6-(x+y) |
| | | Thm*  x,y:Peg. x x,y:Peg. x  y y   otherPeg(x; y) otherPeg(x; y)  Peg Peg |
|
| hanoi_seq_join | Def (s1 @(m) s2)(x) == if x 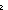 m m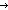 s1(x) else s2(x) fi s1(x) else s2(x) fi |
| | | Thm*  n: n: , m,a,z: , m,a,z: , s1:({a...m} , s1:({a...m}  {1...n} {1...n}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n} {1...n}  Peg). Peg).
Thm* (s1 @(m) s2)  {a...z} {a...z}  {1...n} {1...n}  Peg Peg |
|
| inject | Def Inj(A; B; f) ==  a1,a2:A. f(a1) = f(a2) a1,a2:A. f(a1) = f(a2)  B B   a1 = a2 a1 = a2 |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B). Inj(A; B; f) B). Inj(A; B; f)  Prop Prop |
|
| int_iseg | Def {i...j} == {k: | i | i k & k k & k j } j } |
| | | Thm*  i,j: i,j: . {i...j} . {i...j}  Type Type |
|
| int_upper | Def {i...} == {j: | i | i j } j } |
| | | Thm*  n: n: . {n...} . {n...}  Type Type |
|
| nat | Def  == {i: == {i: | 0 | 0 i } i } |
| | | Thm*   Type Type |
|
| nat_plus | Def  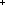 == {i: == {i: | 0<i } | 0<i } |
| | | Thm*  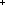  Type Type |
|
| nequal | Def a  b b  T == T ==  a = b a = b  T T |
| | | Thm*  A:Type, x,y:A. (x A:Type, x,y:A. (x  y) y)  Prop Prop |