For integers p, and q  0, the ratio of p to q is the square root of an integer a just when pp = aqq.

We shall consider only the non-negative integers here, so we must show that

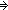
Thm*  a:. prime(a)  (p:, q:. pp = aqq)

It is impossible to build an infinite decreasing sequence of natural numbers, as is expressed by our principle

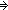
Thm*  P:(Prop). (x:. P(x)  (x':. x'<x & P(x')))  (x:. P(x))

So, to show that a prime number a   has no rational square root, it is enough to show that if you could find a ratio "p/q", expressed with a non-negative numerator, whose square was a, then you could find a smaller such numerator p' of a rational root "p'/q'" i.e.,

p:, q:. pp = aqq  (p':. p'<p & (q':. p'p' = aq'q'))

(see hypothesis Hyp:6 of the proof)

We rewrite

(pp = aqq) to (qq = ap'p')

and then

(qq = ap'p') to (p'p' = aq'q')

giving us a rational square root with numerator p'<p and denominator q'. EXAMPLE

These rewrites are justified by a special-purpose lemma

Thm*  a:. 
Thm*  prime(a)  (p:, q:. pp = aqq  (p':. p'<p & qq = ap'p'))

See the GLOSS of the lemma.

QED

There is also a specialized proof for a = 2. It is simpler but similar.
Thm*  (p:, q:. pp = 2qq) with a gloss.

About: IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html