At: pump theorem 1 1 1 1 1 1 1 1 1 1 1 1 2 1
1. Alph: Type
2. S: ActionSet(Alph)
3. N: 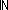
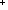
4. s: S.car
5. f: S.car
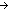
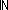 N
N
6. 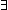 g:(
g:(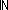 N
N
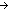 S.car). InvFuns(S.car;
S.car). InvFuns(S.car; 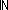 N; f; g)
N; f; g)
7. A: Alph*
8. N < ||A||
9. i: 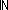 ||A||
||A||
10. j: 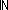 ||A||
||A||
11. i < j
12. (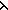 i.f((S:A[||A||-i..||A||
i.f((S:A[||A||-i..||A|| ]
]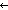 s)))(i) = (
s)))(i) = (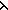 i.f((S:A[||A||-i..||A||
i.f((S:A[||A||-i..||A|| ]
]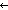 s)))(j)
s)))(j) 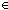
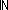 N
N
 A = (A[0..||A||
A = (A[0..||A|| ])
])
By:
InvertRel 0
THEN
BackThru
Thm*  as:T*. (as[0..||as||
as:T*. (as[0..||as|| ]) = as
]) = as
Generated subgoals:None
About: