At: min ar alt 2 2 1 1
1. f: 
2. n:
3. i: (n+1)
4. f(n-i) = f(n)
5. j: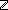 
6. 0 < j
7. j < n-i+1
8. MinAr(f;j+i-1;n) = MinAr(f;j-1;n-i)+i
9. 
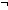f(n-(j+i)) = f(n)
10. f(n-i-j) = f(n-i)
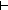MinAr(f;j+i-1;n) = j+i
By:
Assert (n-i-j = n-(j+i))
THEN
RWH (HypC 11) 10
THEN
Thin 11
THEN
Analyze 9
Generated subgoals:None
About:
