Def  A inj B == {f:(AB)| Inj(A; B; f) }

is mentioned by

Thm*  EquivRel on A inj B, same_range_sep(A; B)	[same_range_sep_inj_eqv]
Thm*  same_range_sep(A; B)  (A inj B)(A inj B)Prop	[same_range_sep_wf_inj]
Thm*  (k inj k) ~ (k onto k)	[nsub_inj_ooc_nsub_surj]
Thm*  (k inj k) ~ (k bij k)	[nsub_inj_ooc_nsub_bij]
Thm*  (k inj k) =ext (k bij k)	[nsub_inj_exteq_nsub_bij]
Thm*  (k inj k) =ext (k onto k)	[nsub_inj_exteq_nsub_surj]
Thm*  ((a onto b))  ((b inj a))	[nsub_surj_imp_a_rev_inj2]
Thm*  f:(a onto b). (y.least x:. f(x)=y)  b inj a	[nsub_surj_imp_a_rev_inj]
Thm*  e:(BB).  Thm*  IsEqFun(B;e) Thm*   Thm*  (a:, f:(a onto B). (y.least x:. (f(x)) e y)  B inj a)	[nsub_surj_imp_a_rev_inj_gen]
Thm*  f:(A inj A), i:. f{i}  A inj A	[compose_iter_injection2]
Thm*  k:, f:(k inj k). i:. f{i} = Id  kk	[iter_perm_cycles_uniform2]
Thm*  k:, f:(k inj k). i:. u:k. f{i}(u) = u	[iter_perm_cycles_uniform]
Thm*  k:, f:(k inj k), u:k. i:. f{i}(u) = u	[compose_iter_inj_cycles]
Thm*  (k inj k) ~ (k!)	[nsub_inj_factorial]
Thm*  (a inj b) ~ (b!a)	[nsub_inj_factorial_tail]
Thm*  (b inj b) ~ (b!)	[nsub_inj_factorial2]
Thm*  (A ~ A')  (B ~ B')  ((A inj B) ~ (A' inj B'))	[injection_type_functionality_wrt_ooc]
Thm*  A,B,C:Type, f:(B inj C), g:(A inj B). f o g  A inj C	[compose_wf_inj]
Thm*  a,b:. (a inj b) ~ (b((a-1) inj (b-1)))	[card_nsub_inj_vs_lopped]
Thm*  (A bij B) ~ ((A inj B)(A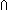 onto B))	[bijtype_ooc_inj_isect_surjtype]
Thm*  (A Discrete)  (k:, f:(k inj A). f  k bij {a:A| i:k. a = f(i) })	[nsub_inj_discr_range_bijtype]
Thm*  (A Discrete) Thm*   Thm*  (k:, f:(k inj A). Thm*  ({a:A| i:k. a = f(i) }  Type Thm*  (& f  k{a:A| i:k. a = f(i) } Thm*  (& Bij(k; {a:A| i:k. a = f(i) }; f))	[nsub_inj_discr_range_bij]
Thm*  ((m inj k))  mk	[inj_typing_imp_le]
Thm*  (A bij B) =ext ((A inj B)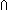(A onto B))	[bijtype_exteq_inj_isect_surjtype]
Thm*  a:, b:, j:b, f:((a-1) inj {x:b| x = j }). Thm*  (i.if i=a-1 j else f(i) fi)  a inj b	[nsub_inj_fill_typing]
Thm*  a:, b:, f:(a inj b). f  (a-1) inj {x:b| x = f(a-1) }	[nsub_inj_lop_typing]
Thm*  (A bij B) 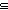 (A inj B)	[bijection_type_inc_inj]
Thm*  (A bij B) 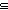 (A inj B)	[bijtype_sub_injtype]
Thm*  (A)  (!(A inj B))	[inj_from_empty_unique]
Thm*  f:(A inj B), a:A. f  {x:A| x = a } inj {y:B| y = f(a) }	[inj_point_deletion_inj]
Thm*  f:(A inj B), a:A. f  {x:A| x = a }{y:B| y = f(a) }	[inj_point_deletion]
Thm*  f:(A inj B). Inj(A; B; f)	[injection_type_injection]
Thm*  f:(A inj B). f  AB	[injection_type_fun]
Thm*  ((A inj B))  (f:(AB). Inj(A; B; f))	[injtype_vs_inj]
Def  Infinite(A) == ( inj A)	[productively_infinite]
Def  Unbounded(A) == k:. (k inj A)	[unboundedly_infinite]

Try larger context: DiscrMathExt IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html